SVEUČILIŠTE U ZAGREBU
FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA
SEMINARSKI RAD
SUSTAV DIGITALNOG POTPISA
Mladen Knežić
0036381733
Zagreb, lipanj 2005
Sadržaj
| 1 Uvod |
| 2 Definicije pojmova |
| 3Digitalni potpis i njegova primjena |
| 3.1Općenito |
| 3.2Postupci kod digitalnog potpisivanja |
| 4 Realizirani sustav digitalnog potpisa |
| 4.1Funkcije kriptiranja/dekriptiranja/sažimanja |
| 4.1.1 Sučelje simetričnih algoritama kriptiranja hr.fer.zemris.crypto.ISim |
| 4.1.2 Sučelje asimetričnih algoritama kriptiranja hr.fer.zemris.crypto.IAsim |
| 4.1.3 Sučelje funkcija za izračunavanje sažetka hr.fer.zemris.crypto.IHash |
| 4.2Funkcije zapisa i čitanja PGP poruka |
| 4.3Grafičko korisničko sučelje |
| 4.4Testovi sustava |
| 5 Simetrični algoritmi kriptiranja |
| 5.1 Općenito |
| 5.2 Princip rada simetričnih algoritama |
| 5.2.1 ECB način kodiranja |
| 5.2.2 CBC način kodiranja |
| 5.2.3 PCBC način kodiranja |
| 5.2.4 CFB način kodiranja |
| 5.2.5 OFB način kodiranja |
| 5.3 Postupak nadopune bloka podataka |
| 5.3.1 PKCS5 padding |
| 5.4 3DES |
| 5.4.1 Općenito |
| 5.4.2 Tehnički podaci |
| 5.4.3 Algoritam |
| 5.4.4 DES algoritam ukratko |
| 5.4.5 Zaključak |
| 5.4.6 Pravni aspekti |
| 5.5 AES |
| 5.5.1 Općenito |
| 5.5.2 Tehnički podaci |
| 5.5.3 Algoritam |
| 5.5.4 Pravni aspekti |
| 5.5.5 Zaključak |
| 5.6 IDEA |
| 5.6.1 Općenito |
| 5.6.2 Tehnički podaci |
| 5.6.3 Algoritam |
| 5.6.4 Pravni aspekti |
| 5.7 SkipJack |
| 5.7.1 Općenito |
| 5.7.2 Tehnički podaci |
| 5.7.3 Algoritam |
| 5.7.4 Pravni aspekti |
| 6 Asimetrični algoritmi kriptiranja |
| 6.1 Općenito |
| 6.2 Pregled implementiranih algoritama |
| 6.3 RSA |
| 6.3.1Općenito |
| 6.3.2 Tehnički podaci |
| 6.3.3 Algoritam |
| 6.3.4 Pravni aspekti |
| 6.4 ElGamal |
| 6.4.1Općenito |
| 6.4.2 Tehnički podaci |
| 6.4.3 Algoritam |
| 6.4.4 Pravni aspekti |
| 6.5 Rabinov kriptosustav |
| 6.5.1Općenito |
| 6.5.2 Tehnički podaci |
| 6.5.3 Algoritam |
| 6.5.4 Pravni aspekti |
| 7 Funkcije za izračunavanje sažetka poruka |
| 7.1 Općenito |
| 7.2 Pregled implementiranih funkcija |
| 7.3 SHA-1 |
| 7.3.1Općenito |
| 7.3.2 Tehnički podaci |
| 7.3.3 Algoritam |
| 7.3.4 Pravni aspekti |
| 7.4 MD5 |
| 7.4.1Općenito |
| 7.4.2 Tehnički podaci |
| 7.4.3 Algoritam |
| 7.4.4 Pravni aspekti |
| 7.5 MASH |
| 7.5.1Općenito |
| 7.5.2 Tehnički podaci |
| 7.5.3 Algoritam |
| 7.5.4 Pravni aspekti |
| 8 PGP format zapisa poruka |
| 8.1 Općenito |
| 8.2 PGP poruke |
| 8.2.1Vrste poruka |
| 8.2.2Struktura poruka |
| 8.2.3Struktura paketa |
| 8.2.4Vrste paketa |
| 8.3 ClearText zapis |
| 8.3.1 ASCII Armor |
| 8.3.2 Primjer ASCII Armor-a |
| 9 Literatura |
Današnji svijet veliku pažnju pridaje informacijama, njihovom rukovanju i zaštiti.
Informacije danas često služe kao izvor prihoda, sredstvo ratovanja, sredstvo zabave.
Kako bi se zaštitile povjerljive informacije te kako bi se onemogućila zlouporaba informacija u vidu čitanja podaci se kriptiraju (transformiraju u oblik nepogodan za čitanje bez znanja dodatnih informacija u vidu ključa kojim su podaci kriptirani) dok se kod sprečavanja mijenjanja podataka najčešće koristi digitalni potpis kod kojeg se izračunava sažetak podataka koji se kasnije kriptira. Kod provjere da li su podaci mijenjani, korisnik prvo izračuna sažetak podataka, zatim kriptira sažetak javnim ključem osobe koja je potpisala dokument te nakraju usporedi dobivene vrijednosti.
U svijetu je vodeći proizvod na području zaštite informacija OpenPGP i njegovi derivati poput GnuPG, PGP, ..
Opisana je vlastita implementacija sustava digitalnog potpisa, s nekoliko različitih algoritama kriptiranja i sažimanja podataka. Naglasak je stavljen na digitalni potpis pa stoga sustav ne nudi enkripciju i dekripciju datoteka kao izdvojen dio već u sklopu digitalnog potpisivanja.
jasni tekst – ulazni podaci algoritama kriptiranja, podaci u netransformiranom obliku
kriptirani tekst – izlazni podaci algoritma kriptiranja, podaci u transformiranom obliku
dodatni blok – dodatni podaci veličine bloka kojeg specificira dani algoritam a služe za inicijalizaciju određenih načina kodiranja
sažetak – podatak određene duljine (najčešće 128 bita) dobiven primjenom funkcije/algoritma sažimanja podataka sa svojstvom da je nemoguće iz njega odrediti podatak za koji je on izračunat te sa svojstvom da promjena jednog bita ulaznog podatka (za koji se izračunava sažetak) uzrokuje značajnu promjenu sažetka
enkripcija / kriptiranje – postupak transformacije jasnog teksta u kriptirani tekst
dekripcija / dekriptiranje – postupak transformacije kriptiranog teksta u jasni tekst, originalni oblik podataka
ključ – podatak koji potpuno određuje transformaciju podataka
tajni ključ – ključ kod simetričnih algoritama, određuje transformacije kriptiranja i dekriptiranja
privatni ključ – ključ kod asimetričnih algoritama, određuje transformaciju kriptiranja i moguće ga je zamijeniti sa javnim ključem (u slučaju zamjene, mijenja se i transformacija iz kriptiranja u dekriptiranje jer jedan ključ služi za kriptiranje dok drugi služi za dekriptiranje)
javni ključ – ključ kod asimetričnih algoritama, određuje transformaciju dekriptiranja te je i njega moguće zamjeniti sa privatnim ključem uz uvjet zamjene transformacije
PGP – Pretty Good Privacy, program za enkripciju podataka, uveo je enkripciju podataka u široku upotrebu i izdržao velike napade usmjerene protiv privatnosti podataka, komercijalna verzija
OpenPGP – open source implementacija, nekomercijalni PGP
runda/prolaz- skup koraka u transformaciji podataka, najčešće se transformacija enkripcije/dekripcije sastoji od nekoliko rundi
Feistelova runda – runda koja specificira značajne izmjene podataka u vidu permutacija i supstitucija bitova
NIST – američka nacionalna ustanova za standarde i tehnologije
NSA – američka nacionalna sigurnosna agencija
Digitalni potpis u današnje doba informatizacije zamjenjuje tradicionalni potpis na digitalnim dokumentima (različite datoteke/informacijski tokovi). Kako bi vjerodostojno zamijenio kasični potpis, digitalni potpis mora osigurati autentičnost potpisa i onemogućiti krivotvorenje potpis.
Koristi se najčešće u svrhu dokazivanja autentičnosti pošiljatelja/vlasnika/autora digitalnog dokumenta.
Kod digitalnog potpisivanja potrebno je prvo izračunati sažetak poruke odnosno dokumenta. Ovisno o odabranom algoritmu, dobit ćemo sažetak određene duljine.
Taj sažetak se zatim dekriptira algoritmom javnog ključa (asimetričnim kriptografskim algoritmom) korištenjem privatnog ključa. Privatni ključ se koristi kako bi svatko tko posjeduje javni ključ, onog tko je potpisao poruku, mogao provjeriti potpis, a kako su postpuci kriptiranja i dekriptiranja jednaki kod asimetričnih algoritama, to znači da će svatko tko javnim ključem kriptira dobiveni potpis (dekripitrani sažetak) dobivene poruke dobiti originalni sažetak.
Kad osoba primi potpisanu poruku, postupak provjere potpisa je sljedeći.
Prvo se izračuna sažetak dobivene jasne poruke. Taj sa žetak se sačuva kako bi se kasnije usporedio.
Zatim se dobiveni potpis (dekriptirani sažetak) kriptira kako bi se dobio sažetak kojeg je osoba koja je potpisala poruku, potpisala. Zatim se te dvije vrijednosti sažetaka usporede i ako su identične, tada je potpis ispravan i autentičnost poruke i njenog pošiljatelja je utvrđena.
Sustav digitalnog potpisa ostvaren je u Java programskom jeziku. Java je izabrana zbog bogate kolekcije funkcija (API), zavidne razine sigurnosti programa ostvarenih u Javi (u smislu izvođenja) te portabilnosti i međuplatformnosti. Java omogućuje korištenje istog bytecode-a (prevedeni tj. kompilirani java programi) na različitim platformama (od osobnih računala, mainframea do ručnih i ugrađenih računala) i operacijskim sustavima (Unix, Linux, Windows, BeOS, MacOS, ...) te nije potrebno posebno prilagođavati program upotrebi na različitim platformama.
Sustav se sastoji od nekoliko java paketa te nekoliko različitih dijelova.
Funkcije kriptiranja/dekriptiranja te izračunavanja sažetaka poruka
simetrični algoritmi kriptiranja smješteni u paketu hr.fer.zemris.crypto.sim koji implementiraju sučelje hr.fer.zemris.crypto.sim.ISim
AES, IDEA, SkipJack, Triple-DES
asimetrični algoritmi kriptiranja u paketu hr.fer.zemris.crypto.asim koji implementiraju sučelje hr.fer.zemris.crypto.asim.IAsim
ElGamal, Rabin, RSA
funkcije za izračunavanje sažetka poruka u paketu hr.fer.zemris.crypto.hash koje implementiraju sučelje hr.fer.zemris.crypto.hash.IHash
MASH, MD5, SHA
pgp funkcije za čitanje i zapis poruka u PGP / OpenPGP u paketu hr.fer.zemris.crypto.pgp
konstante, zapis/čitanje u binarnom obliku, zapis/čitanje u cleartext obliku, apstrakcija PGP paketa, potpisivanje i verifikacija digitalnog potpisa
pomoćne klase i funkcije u paketu hr.fer.zemris.utils
ispis poruka u konzolu
konverzija podataka u Base64 zapis, izračunavanje crc-24 zaštite, faktorizacija cijelih brojeva, logičke operacije xor i or nad poljem byteova, usporedba polja byteova
grafičko korisničko sučelje u paketu hr.fer.zemris.crypto.gui
grafičko sučelje ostvareno korištenjem SWT biblioteke
testovi funkcija kriptiranja/dekriptiranja i izračunavanja sažetka poruka realiziani korištenjem Junit alata
ispitivanje algoritama korištenjem standardnih test vektora te poznatih uzoraka
Sučelje ISim specificira zajedničko sučelje simetričnih algoritama prema korisniku sustava.
Sučelje specificira korištenje sljedećih funkcija
public byte[] decrypt(byte[] in) throws Exception
dekripcija podataka unutar polja byteova
public byte[] encrypt(byte[] in) throws Exception
enkricpija podataka unutar polja byteova
public boolean setKey(byte[] key) throws Exception
postavljanje ključa za enkripciju/dekripciju
public void setParams(Params options) throws Exception
postavljanje parametara algoritma iz objekta
public Params getParams() throws Exception
dohvat parametara iz instance algoritma za ksniju upotrebu
Sučelje IAsim specificira zajedničko sučelje asimetričnih algoritama prema korisniku sustava.
Sučelje specificira korištenje sljedećih funkcija
public byte[] decrypt(byte[] in) throws Exception
dekripcija podataka privatnim ključem unutar polja byteova
public byte[] encrypt(byte[] in) throws Exception
enkripcija podataka javnim ključem unutar polja byteova
public byte[][] genKey() throws Exception
generiranje para javnog i privatnog ključa
public boolean setKey(byte[] pkey, byte[] skey) throws Exception
postavljanje para ključeva
public void setParams(Params options) throws Exception
postavljanje parametara algoritma iz objekta
public Params getParams() throws Exception
dohvat parametara algoritma za kasniju upotrebu
Sučelje Ihash specificira zajedničko sučelje funkcija sažetka prema korisniku sustava.
Sučelje specificira korištenje sljedećih funkcija
public byte[] hash(byte[] data) throws Exception
izračunavanje sažetka podataka iz polja byteova
public boolean setParams(Params options)
postavljanje parametara algoritma iz objekta
public Params getParams() throws Exception
dohvat parametara algoritma za kasniju upotrebu
Funkcije zapisa i čitanja PGP poruka sastoje se od dviju osnovnih klasa, hr.fer.zemris.crypto.input.PGPInput te hr.fer.zemris.crypto.output.PGPOutput .
Ove dvije klase sadržavaju osnovnu funkcionalnost čitanja i pisanja PGP poruka u binarnom obliku. Kako bi se na što jednostavniji način osigurala proširivost sustava mogućnostima zapisa PGP poruka u najrazličitijim oblicima (cleartext, xml i slični oblici), sve funkcije iz ovih klasa pristupaju podacima kroz sučelja. Time je omogućeno da im kao ulazne argumente predamo klasu koja implementira dano sučelje a unutar sebe obavlja kompleksan proces pretvorbe PGP poruka u neki drugi oblik. Primjer ovakve upotrebe su klase PGPArmorOutput i PGPArmorInput koje zapisuju/čitaju PGP poruke u cleartext obliku.
Grafičko korisničko sučelje je u skladu sa samom definicijom potpisa (klasičnog i digitalnog) – brzo, efikasno i uz što manje zahtjeve.
Sučelje pruža nekoliko mogućnosti :
digitalno potpisivanje dokumenata (datoteka)
verifikaciju digitalnog potpisa
rad sa bazom ključeva koje sustav koristi pri radu
dodavanje novih ključeva
generiranje novih ključeva
uklanjanje starih ključeva
Grafičko sučelje izrađeno je okrištenje SWT (standard widget toolkit) biblioteke, open-source java biblioteke napravljene od strane IBM-a.
SWT sučelje stavlja manje zahtjeve na opremu sustava koji izvodi java programe sa grafičkim sučeljem rađenim u SWT-u, no zahtjeva postavljanje dodatnih biblioteka u java okolinu (konkretno se radi o jednoj jar datoteci koju se treba dodati u classpath te 3 dll datoteke koje je potrebno postaviti u java library path – bilo u direktorij u kojem se izvodi java interpreter ili direktorij u kojem se pokreće program koji koristi SWT biblioteku).
Izborom SWT biblioteke, izgled sučelja se približava izgledu radne okoline korisnika (npr. MS Windows, Linux, Unix), što pomaže bržem privikavanju korisnika na rad samog programa.
Testovi kriptografskog dijela sustava (src/crypto kod) realizirani su korištenjem Junit frameworka, koji olakšava pisanje testova. Junit framework zahtjeva pisanje testova na vrlo jednostavan načina u vidu TestCase-a a nudi i grupiranje vište TestCase-ova u jedan TestSuite. TestSuite je također moguće grupirati u drugi TestSuite, što nudi preglednije testove i olakšava testiranje sustava.
Simetrični algoritmi su dobili naziv prema tome što se koristi isti ključ za enkripciju i dekripciju podataka, dok su sami postupci enkripcije i dekripcije najčešće simetrični, tj. postupak dekripcije je jednak postupku enkripcije s tom razlikom što se zamjeni redoslijed operacija.
Simetrični algoritmi nude kraću duljinu ključa uz dovoljnu razinu sigurnosti (u odnosu na asimetrične algoritme), a općenito se smatraju najbržim postupcima kriptiranja podataka. Pokazuju se osjetljivima na brute-force napade zbog kratkog ključa (DES je moguće razbiti u kratkom roku koristeći brute-force metodu).
Simetrični algoritmi se baziraju na izvođenju transformacija nad blokovima podataka.
Općenito se može simetrični algoritam kriptiranja smatrati funkcijom koja mijenja blok podataka iz stanja A u stanje B.
Sam postupak transformacije podataka iz stanja A u stanje B je specifičan za svaki pojedini algoritam, dok je način dobivanja blokova podataka iz ulaznih podataka i komponiranje transformiranih blokova u izlazne podatke zajednički za sve algoritme. Taj način se naziva "način kodiranja" ili "operation mode" odn. "encryption mode".
Načini kodiranja su sljedeći:
ECB electronic code book mode
CBC cypher block chaining mode
PCBC propagating cypher block chaining
CFB cypher feedback mode
OFB output feedback mode
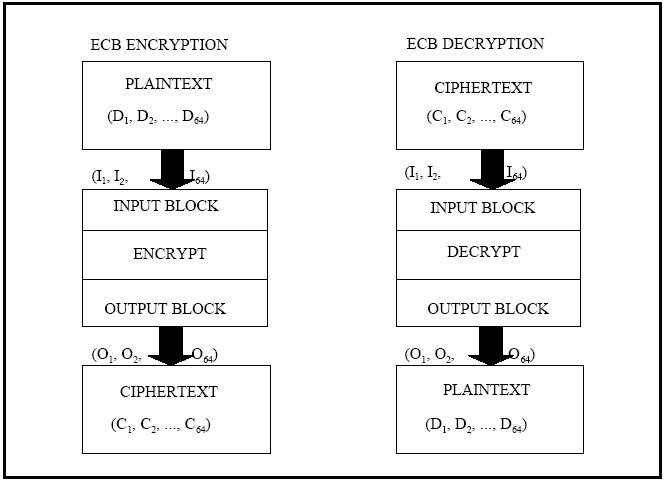
ECB je najjednostavniji način kodiranja, najbrži i prikladno tome podložan napadima.
Ulazni podaci dijele se na blokove veličine koju definira sam algoritam enkripcije. Zatim se dobiveni blokovi transformiraju danim algoritmom, te se novodobiveni blokovi zapišu u izlazne podatke istim redoslijedom kako su se uzimali blokovi iz ulaznih podataka.
ECB način kodiranja prikazan je na sljedećoj slici (napomena – sve varijable su duljine bloka koju specificira dani algoritam).

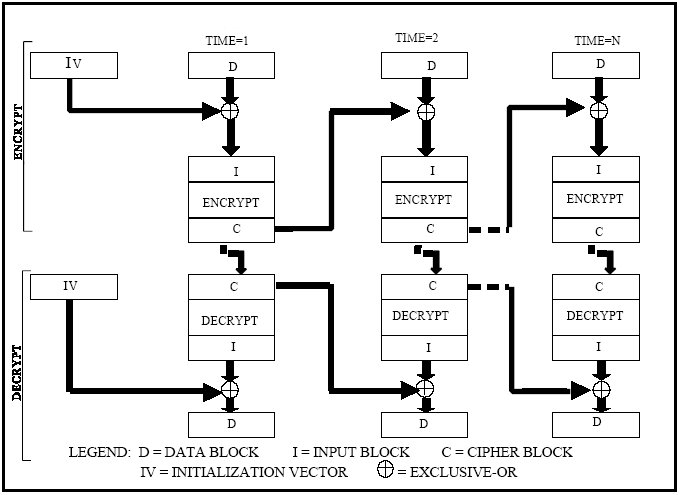
CBC način kodiranja specificira upotrebu dodatnog bloka podataka prilikom svake transformacije bloka ulaznih podataka. Pri prvom bloku ulaznih podataka koristi se blok koji se specificira kao dodatni ulazni podatak, tzv. inicijalni vektor, dok se kod svih ostali blokova koristi prethodno transformirani blok.
Način kombiniranja tog dodatnog bloka je sljedeći – prije transformacije ulaznog bloka, obaviti logičku funkciju xor nad ulaznim blokom i dodatnim blokom te rezultantni blok transformirati i zapisati kao izlazni blok podataka.
CBC način rada prikazan je na sljedećoj slici.
PCBC način kodiranja uvodi još jedan dodatni blok – prethodni ulazni blok podataka, uz to da se za prvi blok podataka on ne koristi.
Prije transformacije ulaznog bloka podataka, ulazni blok se kombinira s prethodnim ulaznim blokom koristeći funkciju xor a zatim se taj rezultat ponovno kombinira istom funkcijom xor ali sada sa prethodnim transformiranim blokom podataka. Rezultantni blok se tada transformira i zapiše kao izlazni blok podataka.
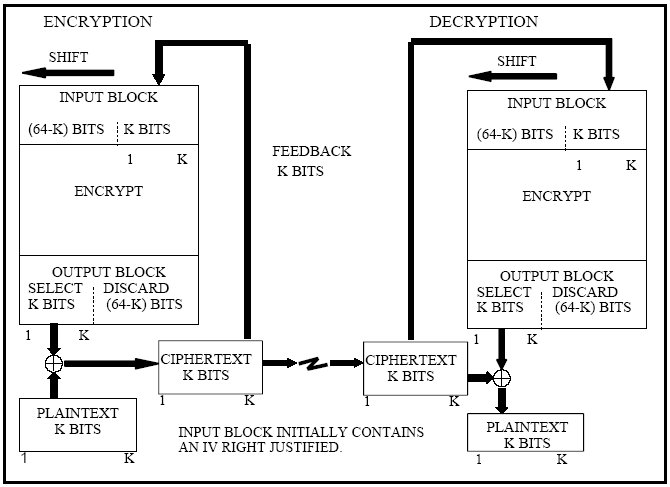
CFB način kodiranja razlikuje se od prethodnih po tome što on ne samo da kombinira već i izvodi dodatnu transformaciju nad dodatnim blokom u vidu posmaka bitova dodatnog bloka.
Prvo se kriptira dodatni blok, koji je na početku jednak inicijalnom vektoru, čijih se K bitova (kriptiranih) kombinira funkcijom xor sa K bitova jasnog teksta. Dobiva se K bitova koji se šalju na izlaz. Dodatni blok se posmiče K bitova ulijevo, a dobivenih K bitova (koje smo postavili na izlaz) nadomješta bitove dodatnog bloka na mjestu koje smo oslobodili posmakom bitova. Na slici je prikazan slučaj kad je veličina bloka 64 bita.
Prema broju bitova koje se dobiva u svakom koraku, ovaj način kodiranja se naziva CFB-K, gdje je K broj bitova. Češće varijante su CFB-8 i CFB-64, kod kojih se u svakom koraku dobiva 8bita odnosno 64bita (najčešće kod algoritama sa 64bitnim blokom, pa se dodatni blok mijenja u potpunosti u svakom koraku).
CFB-8 je dosta prikladan način kodiranja s obzirom da on ustvari predstavlja modifikaciju algoritama kodiranja kod koje nije potrebna nadopuna bloka s obzirom da se uzima po 8bita, a najčešće je upravo 8bita najmanja jedinica podataka (1 byte). Ukoliko se koristi druga verzija npr. CFB-64 , nadopuna je potrebna, jer najčešće podaci nisu poravnati na veličinu koja je višekratnik 64bita već je to 8bita. Zbog općenitosti, u projektu se koristila nadopuna za sve verzije, pa je tako u slučaju CFB-8 kodiranja nadopuna iznosila 8 bita.
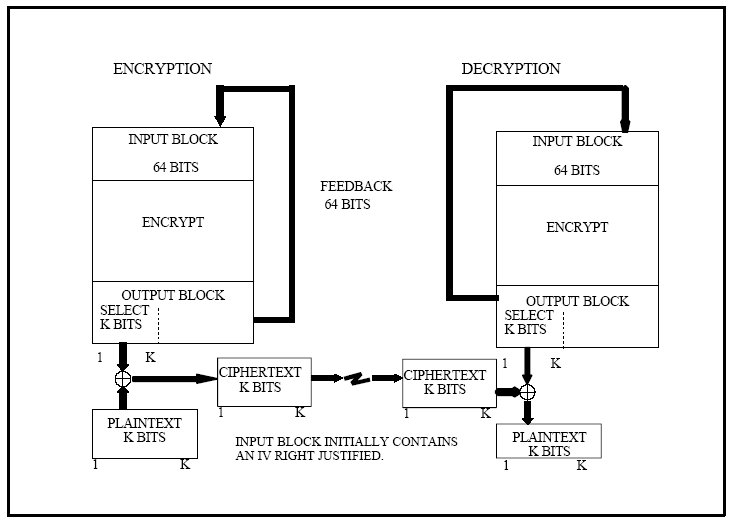
OFB način kodiranja je sličan po principu rada CFB načinu s tom razlikom da se kao nadomjesni bitovi dodatnog bloka uzimaju iz kriptiranog bloka prethodnog bloka podataka.
Prvo se kriptira inicijalni vektor. Kriptirani blok služi kao ulaz za kriptiranje za sljedeći korak algoritma. Iz kriptiranog bloka se uzima K bitova koji se funkcijom xor kombiniraju sa K bitova jasnog teksta te se rezultat od K bitova šalje na izlaz.
Na sljedećoj slici je prikazanOFB način kodiranja za algoritam s veličinom bloka od 64 bita. I ovdje vrijedi napomena da u slučaju ako se koristi OFB-8 tj. OFB način kodiranja sa 8 bitova izlaza, nije potrebna nadopuna. Za sve ostale verzije je potrebna, pa se radi općenitosti u projektu koristila nadopuna i za OFB-8. U tom slučaju je nadopuna uvijek iznosila 8 bita na kraju kriptiranih podataka.
Jedna od zanimljivosti OFB načina kodiranja je i ta da se uopće ne koriste funkcije dekodiranja kriptografskih algoritama. OFB koristi samo funkcije kodiranja kako bi kodirao dodatni blok, kojeg će kombinirati sa jasnim tekstom. Kod dekodiranja, ponovno se kodira dodatni blok i kombinira sa kriptiranim podacima kako bi se dobio jasni tekst.
Ulazni podaci simetričnog algoritma mogu biti bilo koje veličine, dok je veličina bloka podataka danog algoritma fiksno određena.
Zbog toga prilikom podjele ulaznih podataka na blokove dolazi do ostatka podataka nakon podjele u blokove, a koji su veličine manje od veličine bloka podataka.
Kako bi se na jedinstven i jednoznačan način moglo odrediti originalni blok podataka, RSA Laboratories su u dokumentu PKCS #5 [3] predložili način nadopune posljednjeg bloka podataka s veličine manje na veličinu bloka. Taj postupak se najčešće naziva PKCS5 padding.
Specifičnost PKCS5 paddinga je da on ili nadopuni podatke do veličine bloka ili doda novi blok. Npr. ako su ulazni podaci poravnati na veličinu bloka (nakon podjele na blokove, nema ostatka podataka), tada će PKCS5 dodati još jedan blok podataka, a ako je nakon podjele ostalo podataka veličine manje od veličine bloka, tada će ih izmjeniti tako da budu veličine bloka.
Kod postupka skidanja nadopune podataka, nakon dekripcije, vrlo je lako odrediti koji su originalni podaci a što je nadopuna .
PKCS5 padding postupak služi za nadopunu bloka podataka na veličinu zadanu veličinom bloka danog algoritma.
Postupak nadopune:
ulaz : podaci veličine manje ili jednake veličini bloka danog algoritma
postupak :
postavi
M = veličina ulaznih podataka
B = veličina bloka podataka danog algoritma
P = B – (M % B) , P duljine 1B (byte)
postavi
PS = blok podataka koji se sastoji od P byteova od kojih je vaki iznosom jednak P
vrati
blok podataka veličine B koji se sastoji od ulaznih podataka na koje je nadodan blok podataka PS
vidi se da je veličina izlaznog bloka jednaka
duljina = (M %B) + B – (M %B) = B, što je upravo veličina bloka podataka danog algoritma, gdje prvi dio izraza (M%B) predstavlja veličinu ulaznih podataka, a drugi dio veličinu nadodanih podataka
Postupak skidanja nadopune:
ulaz : podaci veličine bloka
postavi :
P = iznos posljednjeg bytea podataka
provjeri
posljednjih P byteova podataka jednaki P
ako nije zadovoljen uvjet, vrati ulazne podatke
inače vrati ulazne podatke bez posljednjih P byteova
3DES (triple-DES ili DES3) je nastao kao odgovor na sve bolje performanse računala koja su dotadašnji standardni kriptografski algoritam DES mogla razbiti u sve kraćem vremenu. Zamjenjuje DES, a specificiran je u FIPS 46-3 [4] .
Zasniva se na DES-u i to u potpunosti. TripleDES koristi za enkripciju DES algoritam, ali s tom razlikom što on kod kriptiranja bloka podataka, koristi 3 poziva DES algoritma s najčeće 3 različita ključa.
Samom konstrukcijom TripleDES-a baziranom na DES dobila se kompatibilnost sa podacima i programima koji su dotada koristili DES, s obzirom da je TripleDES jednak DES-u, ako se izjednače sva tri ključa (jedino što su performanse slabije).
Po performansama TripleDES je sporiji od DES-a, s obzirom da za isti blok podataka on tri puta poziva DES algoritam, te je time i tri puta sporiji, ali to nije problem s obzirom na sve veće performanse računala i dobitkom na sigurnosti podataka.
TripleDES koristi 192-bitni ključ koji se u toku postupka dijeli na 3 ključa po 64 bita, od kojih se pri svakom pozivu koristi samo 56 bita, dok ostatak od 8 bita služi za provjeru samog ključa (paritetni bitovi). Time je ključ efektivno sveden na 168 bita.
Veličina bloka podataka je 64 bita (zbog korištenja DES algoritma).
TripleDES algoritam se oslanja na korištenje DES algoritma koji je opisan u sljedećem poglavlju.
Algoritam enkripcije :
ulaz: DATA ulazni podaci, KEY ključ duljine 192 bita
postupak:
podijeliti ključ KEY na 3 dijela, KEY1, KEY2, KEY3 i to tako da
je KEY = KEY1 : KEY2 : KEY3
pozvati DES enkripciju sa parametrima DATA, KEY1,
izlaz pohraniti u varijablu DATA1
pozvati DES dekripciju sa parametrima DATA1, KEY2,
izlaz pohraniti u varijablu DATA2
pozvati DES enkripciju sa parametrima DATA2, KEY3,
izlaz pohraniti u varijablu DATA3
izlaz : DATA3 izlazni podaci
Algoritam dekripcije:
ulaz: DATA ulazni podaci, KEY ključ duljine 192 bita
postupak:
podijeliti ključ KEY na 3 dijela, KEY1, KEY2, KEY3 i to tako da
je KEY = KEY1 : KEY2 : KEY3
pozvati DES dekripciju sa parametrima DATA, KEY3,
izlaz pohraniti u varijablu DATA1
pozvati DES enkripciju sa parametrima DATA1, KEY2,
izlaz pohraniti u varijablu DATA2
pozvati DES dekripciju sa parametrima DATA2, KEY1,
izlaz pohraniti u varijablu DATA3
izlaz : DATA3 izlazni podaci
DES algoritam koristi veličinu bloka od 64 bita, koriste se ključevi duljine 64 bita s time da je ključ efektivne veličine 56 bita jer se 8 bita ključa koristi radi provjere samog ključa (paritetni bitovi).
Prije same enkripcije potrebno je postaviti 16 48-bitnih podključeva.
Sam postupak postavljanja ključeva sastoji se u tome da se određenim permutacijama ključa dobije 16 podključeva veličine 48 bita. Izrazi se ne navode već je potrebno pogledati u specifikaciji DES algoritma, [2].
Postupak enkripcije bloka podataka DES algoritmom:
ulaz : blok podataka veličine bloka DES algoritma
permutirati ulazni blok
podijeliti blok na dva dijela L i R, L lijevh 32 bita, R desnih 32 bita bloka podataka
u 16 jednakih koraka izvršiti transformaciju nad L i R prema izrazima
Li = Ri-1
Ri= Li xor f(Ri-1, Ki)
izlaz: R16:L16
Postupak enkripcije bloka podataka DES algoritmom:
ulaz : blok podataka veličine bloka DES algoritma
permutirati ulazni blok
podijeliti blok na dva dijela L i R, L lijevh 32 bita, R desnih 32 bita bloka podataka
u 16 jednakih koraka izvršiti transformaciju nad L i R prema izrazima
Li = Ri-1
Ri= Li xor f(Ri-1, Ki)
izlaz: R16:L16
TripleDES je nastao kao relativno elegantno i bezbolno rješenje problema duljine ključa DES-a, kao algoritam koji će biti kompatibilan s već postojećim sustavima.
Može se reći da je TripleDES uspio donekle u svojim namjerama, jer je podigao razinu sigurnosti podataka no isto tako se njegovim neuspjehom može smatrati jedino njegova brzina koja je u odnosu na DES tri puta manja (zbog tri poziva DES algoritma za svaki blok podataka koji se obrađuje).
TripleDES je razvio Walter Tuchman(voditelj razvoja DES algoritma pri IBM-u ) i standardiziran je u FIPS 46-3 [4].
Advanced Encryption Standard, kraće AES, nastao je kao službeni nasljednik DES-a.
AES se bazira na Rijndael algoritmu, a specificiran je u FIPS 197 [4].
Kako bi bio što brži, dizajniran je tako da se sve operacije provode nad byteovnim podacima.
Koriste se ključevi dužine 128, 192 ili 256 bita, pa ga se ovisno o primjenjenoj dužini ključa ponegdje naziva AES-128, AES-192, AES-256.
Koristi se blok veličine 128 bita kako je definirano standardom, no Rijndael algoritam omogućava korištenje blokova duljine 128, 192 i 256 bita.
Koristi se varijabilan broj prolaza algoritma, ovisno o duljini ključa i bloka. Ako su blok i ključ veličine 128 bita, tada se koristi 9 prolaza. Ako je ključ ili blok veličine 192 bita te nijedan nije duži od 192 bita, tada se koristi 11 prolaza, dok se u slučaju da je ključ ili blok veličine 256 bita koristi 13 prolaza.
AES na početku rada izračunava prošireni ključ kako bi se dobilo dovoljno podključeva od kojih će se svki koristiti samo jednom pri pozivu funkcije AddRoundKey.
AES pri radu koristi nekoliko funkcija kojima mijenja tzv. state, tj blok podataka nad kojima se trenutno vrši kriptiranje/dekriptiranje. State je veličine jednog bloka.
Funkcija ShiftRows mijenja state tako da ga posloži u tablicu s 4 retka, a zatim posmiče stupce za određen broj bitova.
Funkcija MixColumns mijenja state tako da ga posloži u tablicu s 4 retka. Smatrajući tablicu matricom, vrši se množenje tablice s određenom matricom veličine 4 x 4.
Funkcija AddRoundKey vrši logičku operaciju XOR nad state i dijelom proširenog ključa.
Funkcija ByteSub mijenja byteove unutar state-a sa byteovima definiranima u dvije tablice, jedna za enkripciju druga za dekripciju.
Budući je AES iterativni algoritam koji transformacije izvodi u nekoliko rundi, ovisno o veličini ključa / bloka, jedna iteracija izgleda ovako :
AddRoundKey
ByteSub
ShiftRow
MixColumn
Jedna iteracija naziva se runda, a posljednja runda kod enkripcije se razlikuje u tome da se ne poziva funkcija MixColumn.
Razvijen od Joan Daemena i Vincenta Rijmena iz Belgije. Standardiziran u Sjedinjenim Američkim Državama kao Advanced Encryption Standard.
Dobar, jak algoritam kojem se predviđa duga i široka upotreba. Samim postupkom standardizacije kao američki standard za zaštitu informacija dokazao se kao siguran algoritam koji će i mnoge druge zemlje/osobe prihvatiti kao takav.
Punim nazivom International Data Encryption Algorithm, IDEA se u svom sadašnjem obliku koristi od 1992. godine. Starije verzije su poznate pod nazivima PES (Proposed Encryption Standard) te IPES (Improved PES).
Koristi se u PGP-u, a do danas nije poznati način uspješnog napada na sigurnost podataka zaštićenih ovim algoritmom.
Veličina bloka je 64 bita, ključ je 128-bitni.
U toku rada koriste se 52 16-bitna podključa, koji ujedno čine razliku između dekripcije i enkripcije.
Ulazni podaci (blok od 64 bita) dijeli se na 4 16 bitna bloka. Zatim se u 8 prolaza algoritma, podaci kombiniraju sa podključevima i međusobno. U posljednjem, devetom prolazu kombiniraju se ta četiri bloka i četiri posljednja podključa.
Algoritmi enkripcije i dekripcije su identični s tom razlikom što se koriste različiti podključevi. Za enkripciju treba 52 podključa a isto toliko i za dekripciju. Izračunavanje podključeva traje određeno vrijeme, ali kako se podključevi izračunavaju samo prilikom postavljanja ključa, to nije problem.
Algoritam generiranja podključeva je sljedeći :
podijeliti ključ na 8 blokova po 16 bita i to je prvih 8 podključeva
rotirati ulijevo ključ za 25 bita, ponovno podijeliti i opet imamo novih 8 podključeva
ponoviti rotaciju i podjelu još 4 puta
rotirati ključ i uzeti prva 4 bloka po 16 bita za posljenja 4 podključa
na osnovu dobivenih podključeva, generirati podključeve za dekripciju i to tako da su oni ili aditivni ili multiplikativni inverzi podključeva koje smo prethodno generirali
Autori algoritma su Xuejia Lai i James Massey .
Algoritam je patentiran i komercijalna upotreba nije dozvoljena bez odobrenja (licence).
Namijenjen za kriptiranje povjerljivih telekomunikacijskih tokova.
Veličina bloka podataka je 64 bita. Veličina ključa je 80 bita.
SkipJack prilikom enkripcije koristi dva pravila prilikom enkripcije / dekripcije.
Pravila su nazvana A i B i primjenjuju se nad 4 riječi tj. 4 podatka od 2 bytea (ulazni podatak se dijeli na 4 dijela) – w1, w2, w3, w4, te se koristi i brojač koji je podatak veličine 2 bytea.
Pravilo A :
permutirati w1
nova vrijednost w1 je rezultat xor funkcije nad permutiranim w1, brojačem i w4
w2 postaje w3, a stari w3 postaje w4
w2 je permutacija w1 iz 1. koraka
brojač se uveća za 1
Pravilo B:
permutirati w1
w2 je permutirani w1
w3 je rezultat funkcije xor između starog w1, brojača i w2
w4 je stari w3
w1 je stara vrijednost w4
brojač uvećati za 1
Korištenjem naizmjenično pravila kriptira se podatak od 64 bita.
Kod dekripcije, koriste se inverzna pravila A' i B', koja su funkcijski inverzi
pravila A i B.
Kriptiranje se provodi u 32 koraka. Izvede se 8 koraka pravila A, zatim 8 koraka pravila B. Zatim se još 8 puta izvede A i 8 puta B.
Dekriptiranje se provodi obrnutim redoslijedom.
Standardiziran u FIPS 185 [13} od strane NIST-a, predložen od strane NSA.
Asimetrični algoritmi temelje se na konceptu para ključeva, javnog i privatnog. Osnovne pretpostavke algoritma koji nosi naziv asimetrični kriptografski algoritam je da se iz javnog ključa ne može dobiti privatni ključ, na niti jedan poznati ili nepoznati način.
Snaga asimetričnih algoritama svodi se na rad s velikim prostim brojevima (tipično su to brojevi koji imaju preko 1024 binarne znamenke), koji se različitim načinima povezuju u parove koji omogućuju enkripciju podataka jednim ključem iz para a dekripciju drugim ključem iz para. Da bi se na osnovu jednog ključa izračunao drugi ključ, potrebno je jako mnogo vremena zbog toga što se postupci svode na faktorizaciju velikih prostih brojeva, što je vremenski zahtjevna operacija a i sam postupak faktorizacije nije razvijen u nekoj optimalnoj mjeri.
RSA enkripcija donijela je revoluciju u svijet kriptografije. Prva je predložila upotrebu para javnog i privatnog ključa i time značajno pridonijela sigurnosti komunikacije. Korištenje para ključeva donosi razne pogodnosti, od toga da možemo slobodno objaviti javni ključ bez straha da bi netko iz njega mogao doznati privatni ključ, možemo mijenjati javni i privatni ključ u svrhu enkripcije/dekripcije datoteka.
RSA koristi par javnog i privatnog ključa, koji se zapisuju u obliku n,e te n,d .
Može se zamijeniti javni i privatni ključ kod enkripcije/dekripcij bez ikakvih problema. Isto tako može se zamijeniti funkcije kriptiranja / dekriptiranja jer su posve identične, no potrebno je paziti kod pretvorbe podataka u niz brojeva kako bi uvijek znali koji dio podataka je predstavljen kojim brojem.
Odaberu se dva velika prosta broja p i q.
Izračunaju se brojevi n i z kao :
n = p * q,
z = (p-1) * (q-1).
Odabere se broj e manji od z i relativno prost s obzirom na z ( tj. nzm(e,z) = 1 ).
Izračuna se d tako da vrijedi
(e * d ) mod z = 1 , tj. e * d = k * z + 1,
Par brojeva n,e proglasi se javnim ključem, a par n,d privatnim ključem.
Postupak kriptiranja svodi se na pretvorbu poruke u zapis niza brojeva manjih od n, te se svakog od njih predstavljenog kao broj M pretvori u kriptirani oblik, C formulom
C = Me mod n
Postupak dekripcije je jednak, samo se sada koristi privatni ključ n,d
M = Cd mod n.
RSA algoritam su razvili Ron Rivest, Adi Shamir i Len Adelman. Algoritam su nazvali po inicijalima svojih prezimena, a ujedno su i stvorili tvrtku RSA Data Security koja se bavi razvojem sigurnosnih programa. RSA Data Security je vlasnik RSA algoritma a slobodna implementacija nalazi se u PGP-u i GNU PG-u čiji je izvorni kod slobodno dostupan .
ElGamal algoritam kriptiranja je alternativa RSA algoritmu, nešto je složeniji za izvedbu nego RSA.
ElGamal koristi
Odabere s p veliki prosti broj. Odaberu se dva slučajna broja g i x manja od p.
Izračunamo y = gx mod p .
Trojku (y, g, p) proglasimo javnim ključem, a par (p, x) privatnim ključem.
Podatke ponovno kriptiramo tako da ih pretvorimo u zapis brojeva manjih od p, predstavljene oznakom M. Odaberemo slučajni broj k manji od p-1 i relativno prost sa p-1. Bez poznavanja broja k nije moguće dekriptirati poruku pa ga zato i šaljemo kao broj b, dok je a poruka koja je kriptirana.
a = gk mod p
b = ykM mod p
Kriptirani tekst sastoji se on niza brojeva računatih kao a za svaki broj iz poruke, te broj b koji omogućuje dekriptiranje poruka.
Postupak dekriptiranja je:
M = b/ax mod p.
ElGamal je osmišljen 1985. godine, autor je T. ElGamal. Slobodan je za upotrebu i nalazi se u PGP i GNU PG programima.
ElGamal se češće koristi jer nema pravnih ograničenja poput RSA algoritma.
Rabinov kriptosustav je prvi koji je dokazano siguran algoritam javnog ključa.
Dokazivo je da je postupak dobivanja poruke iz dane kriptirane poruke bez znanja ključa dekripcije računski ekvivalentno faktorizaciji velikog prostog broja koji se koristio kod kriptiranja, modulus.
Koristi se par ključeva, javni n, privatni ključ je par p,q.
Intenzivno se koriste operacije računanja kvadratnih korijena no to je još uvijek brže od RSA algoritma. Enkripcija je brža barem dva puta, dok je dekripcija usporediva brzinom sa dekripcijom kod RSA algoritma.
Odabrati dva velika, slučajna, međusobno različita prosta broja p i q, približno jednake veličine.
Izračunati n = p * q .
Javni ključ je n, privatni ključ je par p,q.
Enkripcija se svodi na predstavljanje poruke kao niz brojeva manjih od n.
Kriptirana poruka sastoji se od niza brojeva c, računatih kao
c = m2 mod n, gdje broj m reprezentira dio poruke.
Dekripcija je složenija jer treba naći 4 kvadratna korijena m1, m2, m3, m4 od primljene poruke tj. broja c. U određenim slučajevima dobivaju se samo dva kvadratna korijena. Najveći problem je odrediti koja je poruka od 4 korijena original, tj. koja je poslana, a koje su krive. U izrađenom sustavu, određivanje se svelo na izračunavanje checksuma tj. jedinstvene brojke koja određuje svaku poruku, koji se dodavao poruci prije kriptiranja te se kod dekriptiranja provjeravalo ako poruka zadovoljava računati checksum.
Autor je Michael Rabin i slobodan je za upotrebu (royalty-free) .
Funkcije za izračunavanje sažetka poruka služe za izračun jedinstvenog broja određene duljine koji karakterizira neki niz znakova, ali na taj način da iz njega nije moguće odrediti niz znakova za kojeg je on izračunat.
Sažetak poruke koristi se kod digitalnog potpisa u svrhu detekcije mijenjanja izvorne poruke, jer u slučaju promjene jednog bita unutar poruke, sažetak je bitno drugačiji, najčešće je razlika u više od nekoliko bitova sažetka.
SHA, je skraćenica od Secure Hash Algorithm tj. sigurni algoritam za izračunavanje sažetka.
SHA funkcija je alternativa MD klasi funkcija sažetaka (MD4, MD5). Stvara duži sažetak nego MD5. U novije vrijeme javljaju se revizije koje daju još duži sažetak kako bi se pojačala sigurnost. U novije vrijeme pojavila se uzbuna zbog navodnog probijanja SHA algoritma, no nije bilo tako. Desilo se ono što je bilo i očekivano zbog duljine sažetka od 160 bitova, a to je da su nađene dvije različite poruke koje daju isti sažetak. To nije problem jer je uistinu teško naći poruku koja je smislena u odnosu na prvu a da ima isti sažetak. Problem bi bio kad bi za određeni sažetak mogli odrediti poruku koja generira takav sažetak, što nije bio slučaj u navedenom primjeru.
Stvara 160 bitni sažetak. Postoje razne verzije (SHA-1, SHA-256, SHA-383,
SHA-512, double SHA) koje daju različite veličine sažetaka.
Izvodi se nad blokovima podataka od 512 bita, pa se manji blokovi nadopunjuju poznatim pravilima na 512 bita (koristi se postupak predložen uz MD5 algoritam tako da se na kraj podataka doda bit 1 a zatim toliko bitova 0 da ostane još 64 bita mjesta za upis duljine originalne poruke, ako nema dovoljno mjesta tada se dodaje još jedan blok).
SHA postupak sastoji se od 4 kruga s dvadeset koraka. Koristi se samo 4 konstante ( u svakom koraku po jedna). Koriste se i četiri nelinearne funkcije, isto tako u svakom koraku po jedna.
Postupak se sastoji u tome da se iz poruke veličine 512 bita izračuna 80 riječi po 32 bita. Nad tim riječima izvodi se sam postupak od 80 koraka te se na kraju dobiva sažetak veličine 160 bitova.
Standardiziran kao ANSI standard X9.30 part 2.
MD5 (Message digest 5 tj. sažetak poruke 5) je najčešće korišteni hash algoritam. 1996. godine otkrivene su mu slabosti, pa se ipak preporuča korištenje SHA algoritma.
Nastao je na temelju prijašnjih algoritama, MD4 i MD2 no i kod njih su pronađeni nedostaci pa se ni oni ne koriste.
Najčešća upotreba je na internetu, gdje se često daju sažetci određenih dokumenata kako bi se potvrdila njihova autentičnost. No i u tom slučaju, MD5 sažetak najčešće stoji uz SHA sažetak.
Stvara 128 bitni sažetak te je bitno nesigurniji od SHA. Ne preporuča se njegova upotreba zbog otkrivenih slabosti.
Postupak se sastoji od četiri kurga po 16 koraka.
U svakom krugu koristi se druga nelinearna funkcija nad dijelom podataka.
Svaki blok podataka dijeli se na 16 podblokova, od kojih svaki sudjeluje u izračunavanju sažetka 4 puta. U svakom koraku koristi se i 32-bitna konstanta a sažetak se inicijalizira sa 4 konstante.
Na kraju se dobiva 128-bitni sažetak.
Algoritam je osmislio Ron Rivest (jedan od autora RSA algoritma), a distribuira ga RSA Data Security. Slobodan je za upotrebu i ne treba kupovati licencu.
MASH (Modular arithmetic secure hash ili sigurni sažetak u modularnoj aritmetici) je najnoviji smjer kretanja u području hash funkcija.
Bazira se na konstrukciji iterativne funkcije korištenje operacija mod M kao osnova sažimanja podataka.
Ove funkcije karakterizira mala brzina te nepovjerenje zbog prethodnih prijedloga koji su se dokazali kao nesigurni.
MASH-1 i MASH-2 funkcije zasada nisu pokazale slabosti a i brzina im je zadovoljiva.
Osnovna karakteristika ovih funkcija je odabir dužine sažetka ovisno o zahtjevanoj razini sigurnosti – što je veći modulus M to je duži sažetak a time i veća sigurnost.
Generira se sažetak duljine jednake duljini modulusa M. Kod izračunavanja sažetka potrebno je odrediti modulus te ga je ujednopotrebno i prenositi kao parametar uz izračunati sažetak, a moguće je i definirati vlastiti algoritam jednak MASH-1 ili MASH-2 funkciji uz obaveznu definiciju modulusa kao određen broj pa će se uvijek dobiti sažetak iste duljine a modulus nije potrebno prenositi kao parametar.
Razlika između MASH-1 i MASH-2 funkcija je u eksponentu – kod sažimanja MASH-1 koristi eksponent 2 dok MASH-2 koristi eksponent 28+ 1.
Sigurnost im se bazira ne težini izračunavanja modularnih korijena (zbog toga i razlika u eksponentu).
Odabrati dva tajna, slučajna prosta broja p i q duljine m-bita te izračunati M kao
M = p * q .
Definira se H0=0 i A=0xf000.....0, n-bitovne konstante
Definira se duljina n-bita gdje je n najveći višekratnik od 16 a manji od m.
Blok koji se sažima nadopuni se s bitovima 0 na veličinu t*n/2, uz najmanji dopušteni t jednak 1. Nadopunjeni blok se dijeli u n/2 – bitne blokove x. Zadnji blok x se dodaje
kao n/2–bitovna reprezentacija duljine izvorne poruke b
Svaki se x-blok dijeli na 4-bitne dijelove a zatim se proširuju na 8 bita dodajući im
4-bitne konstante i tvori y-blok .
Broj H u i-tom koraku je funkcija prethodnog broja H, trenutnog bloka y i konstante A, kvadrirano modulo M uzimajući lijevih n bitova te dodatno vršeći operaciju xor sa prethodnim brojem H.
Sažetak je n-bitni broj H u posljednjem koraku.
MASH funkcije su definirane u dokumentu
ISO/IEC 10118 – Part 4 : Hash functions using modular arithmetic [14], i slobodno se koriste.
PGP je postao de-facto standardom razmjene digitalnih poruka u zaštićenom obliku.
Iako često izložen napadima, PGP je opstao i nastavio sa razvojem. Rezultati razvoja su vidljivi u tome da PGP prati najnovije smjernice na području zaštite podataka. Kao primjer može se navesti rano uvođenje najnovijih kriptografskih algoritama u PGP sustav te rezervacija mjesta u kodu za algoritme koji se tek razvijaju (npr. rezervacija packet taga za eliptičke krivulje i double SHA iako neki od njih nisu ni definirani standardom).
Da je PGP na dobrom putu, potvrđuje i njegova opensource, freeware verzija GNU PG , tj. GPG (GNU Privacy Guard) te OpenPGP, udruženje koje aktivno razvija OpenPGP standarde.
PGP specificira sljedeće poruke :
kriptirana poruka
potpisana poruka
komprimirana poruka
literalna poruka
Najzanimljivija je potpisana poruka, jer definira digitalni potpis što je i tema ovog rada dok su ostale poruke manje važne i nisu cilj proučavanja.
Potpisana poruka u sebi nosi sam digitalni potpis, oznaku verzije, vrijeme potpisivanja, oznake algoritma javnog ključa i sažimanja podataka. Potpisana poruka nosi i podatke koji omogućuju brzu identifikaciju neispravnih ili krivotvorenih poruka, bez potrebe za dužim postupcima ispitivanja neispravnosti poruka.
Kriptirana poruka nosi unutar sebe kriptirane podatke i podatke o samoj enkripciji (identifikator ključa, korišteni algoritmi i slični).
Komprimirana poruka sadrži komprimirane podatke koji nakon dekompresije postaju ispravna PGP poruka.
Literalna poruka služi kao omotnica za podatke koje smo potpisali. Cilj digitalnog potpisa nije tajnost poruke već autentičnost.
PGP poruke sastloje se od manjih jedinica, paketa. Paketa ima nekoliko vrsta a svaki definira svoju vlastitu strukturu tijela paketa, dok je zaglavlje paketa jednako za sve.
PGP poruke se sastavljaju jednog ili više paketa koristeći sljedeća pravila :
PGP poruka =
kriptirana poruka | potpisana poruka | komprimirana poruka |
literalna poruka
kriptirana poruka =
simetrično kriptirani paket |
sekvenca kriptiranog sjedničkog ključa, simetrično kriptirani paket
sekvenca kriptiranog sjedničkog ključa =
kriptirani sjednički ključ |
sekvenca kriptiranog sjedničkog ključa, kriptirani sjednički ključ
kriptirani sjednički ključ =
sjednički ključ kriptiran javnim ključem |
simetrično kriptirani sjednički ključ
komprimirana poruka = komprimirani paket
literalna poruka = literalni paket
potpisana poruka =
paket potpisa, PGP poruka | poruka potpisana jednim potpisom
poruka potpisana jednim potpisom =
paket jednog potpisa, PGP poruka, paket potpisa
Paket se sastoji od zaglavlja i tijela.
Zaglavlje se sastoji od dva ili više okteta. Prvi oktet specificira tip paketa i verziju.
Starije verzije (prije verzije 4) su još dodatno specificirale i broj okteta duljine paketa.
Nakon prvog okteta dolazi 1, 2 ili 4 okteta duljine paketa. Moguće je da duljina paketa bude neodređena te u tome slučaju treba duljinu paketa odrediti na neki drugi način.
Tijelo paketa je specifično za svaki paket. Najčešće se tu specificira verzija paketa, vrijeme kreiranja paketa, oznake algoritama i ključeva, te sam digitalni potpis
Navest će se samo nekoliko vrsta paketa koji čine samu potpisanu poruku.
To su paket jednog potpisa, literalni paket te paket potpisa .
Paket jednog potpisa sastoji se od redom :
okteta verzije paketa
okteta vrste potpisa (binarni dokument, tekstualni dokument i slično)
okteta oznake algoritma sažimanja
okteta oznake algoritma javnog ključa
8 okteta oznake ključa
okteta ugnježđenog potpisa – specificira da dolazi još više ovakvih paketa tj. mogućnost više potpisa nad jednim dokumentom
Literalni paket se najčešće javlja kao PGP poruka unutar potpisane poruke.
Sastoji se redom iz :
okteta oznake formata (binarni, tekstualni podaci)
okteta duljine naziva dokumenta (datoteke)
niza okteta koji čine naziv datoteke
4 okteta koij označavaju vrijeme nastanka, promjene dokumenta ili trenutno vrijeme ako nema smisla navoditi vrijeme
Paket potpisa ima dvije verzije i ovdje se navodi verzija 3, koju je trenutno važeća, dok se verzija 4 rijetko koristi u novijim proizvodima.
Sastoji se redom od :
okteta oznake verzije
okteta koji specificira duljinu sljedeća dva polja
okteta oznake vrste potpisa
4 okteta vremena nastanka potpisa
8 okteta oznake ključa
okteta oznake algoritma javnog ključa
okteta oznake algoritma sažimanja
dva okteta dobivena kao dva lijeva okteta iz samog sažetka kako bi se brzo otkrili neispravni potpisi
jedan ili više velikih cijelih brojeva koji definiraju sam potpis
Veliki cijeli broj zapisuje se kao redom :
dva okteta zapisa bitovne duljine broja
niz okteta takvih da je cijeli broj zapisan u njima
Cleartext zapis je specijalna verzija PGP poruke namijenjena za prijenos preko mreže ili drugdje gdje dolazi do konverzije podataka iz jednog zapisa u drugi (tipično promjena kodne stranice).
Cleartext zapis specificira korištenje samo ASCII znakova, pretvorbu binarnih podataka u niz Base64 (Radix-64) kodiranih znakova te dodavanje dodatnih tekstualnih zaglavlja poznatijih kao ASCII armor.
Base64 zapis je standardni zapis kod kojeg se 3 okteta bilo koje kodne stranice pretvaraju u 4 okteta u ASCII kodu i to samo one znakove koje je moguće ispisati na zaslon ili papir. Detalji nisu spominjani jer je Base64 zapis detaljno specificiran Internet standardima a i sama izvedbena okolina Jave ima vlastitu implementaciju.
ASCII armor je vrsta zapisa kod kojeg se binarni podaci zapisuju tekstualno.
Podacima prethodi početno zaglavlje, opcionalna zaglavlja, obavezni prazni red. Zatim slijede podaci nakon kojih ide kodirani checksum u obliku CRC24 koda, pretvorenog u Base64 zapis kojemu prethodi znak '='.
Nakon toga dolazi završno zaglavlje.
Primjer početnog zaglavlja je :
-----BEGIN PGP MESSAGE-----
dok je završno zaglavlje jednako početnom s time da je riječ BEGIN zamijenjena sa riječi END.
Potpisane poruke dolaze u nešto izmjenoj formi :
početno zaglavlje je promjenjeno u
-----BEGIN PGP SIGNED MESSAGE-----
jedno ili više opcionalnih zaglavlja
obavezan prazni redak
jasni tekst potpisane poruke
cleartext oblik potpisa (BEGIN PGP MESSAGE zaglavlje, poruka, završno zaglavlje poruke)
završno zaglavlje potpisane poruke.
U slučaju potpisane poruke u cleartext obliku, podrazumijeva se upotreba MD5 algoritma, ako nije u opcionalnom zaglavlju drugačije specificirano.
Opcionalna zaglavlja se sastoje od naziva i vrijednosti zaglavlja koji se razdvajaju
zankom ': ' tj. dvotočka i praznina.
Definirana opcionalna zaglavlja :
Version – definira verziju OpenPGP-a koji je kreirao poruku
Comment – korisnički komentar
MessageID – niz zankova koji treba biti jedinstven za ovu poruku
Hash – lista zarezom odvojenih vrijednosti
Charset – kodna stranica
Definirana početna zaglavlja su :
BEGIN PGP MESSAGE – općenite PGP poruke
BEGIN PGP PUBLIC KEY BLOCK – za razmjenu ključeva
BEGIN PGP PRIVATE KEY BLOCK – za razmjenu ključeva
BEGIN PGP SIGNATURE – potpisane poruke
BEGIN PGP MESSAGE, PART X/Y – poruke u više dijelova
BEGIN PGP MESSAGE, PART X – poruke u više dijelova sa nepoznatim brojem ukupnih dijelova
Primjer je preuzet iz OpenPGP specifikacije.
-----BEGIN PGP MESSAGE-----
Version: OpenPrivacy 0.99
yDgBO22WxBHv7O8X7O/jygAEzol56iUKiXmV+XmpCtmpqQUKiQrFqclFqUDBovzS
vBSFjNSiVHsuAA==
=njUN
-----END PGP MESSAGE-----
[1] DES Modes of Operation,
FIPS PUB 81, December 2, 1980.,
www.itl.nist.gov/fipspubs
[2] Data Encryption Standard (DES),
FIPS PUB 46-2, December 30, 1993.,
www.itl.nist.gov/fipspubs
[3] PKCS #5 v2.0: Password-Based Cryptography Standard,
RSA Laboratories, March 25, 1999.,
www.rsasecurity.com/rsalabs/
[4] Data Encryption Standard (DES),
FIPS PUB 46-3, December 30, 1993.,
www.itl.nist.gov/fipspubs
[5] Advanced Encryption Standard (AES),
FIPS PUB 197, November 26, 2001.,
www.itl.nist.gov/fipspubs
[6] Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone, Handbook of Applied Cryptography, CRC Press, Fifth printing, Kolovoz 2001, dostupno na Internet adresi http://www.cacr.math.uwaterloo.ca/hac/
[7] PKCS 1,3,5,6,7,8,9,10,11,12,15, Public key cryptography standard
RSA Laboratories, March 25, 1999.,
www.rsasecurity.com/rsalabs/
[8] Leo Budin, RSA, Skripta iz Operacijskih sustava 2, Ožujak 2001.
[9] Darrel Hankerson, Alfred Menezes, Scott Vanstone, Guide to Elliptic Curve Cryptography, Springer-Verlag New York Inc.,
springeronline.com
[10] Elisabeth Oswald, Introduction to Elliptic Curve Cryptography, Srpanj 2002, http://www.iaik.tu-graz.ac.at/aboutus/people/oswald/papers/Introduction_to_ECC.pdf
[11] Ron Rivest, The MD5 Message-Digest Algorithm, Travanj 1992,
ftp://ftp.rfc-editor.org/in-notes/rfc1321.txt
[12] The MASH Hash Functions, v.1.1, Bart Preneel, K.U.Leuven, May 15, 2004
[13] Escrowed Encryption Standard (EES, SkipJack),
FIPS PUB 185, February 9, 1994.,
www.itl.nist.gov/fipspubs
[14] ISO/IEC 10118 – Part 4 : Hash functions using modular arithmetic
[15] RFC-2440 OpenPGP Message Format , www.ietf.org