SVEUČILIŠTE U ZAGREBU

FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA

SEMINAR IZ PREDMETA OPERACIJSKI SUSTAVI 2

ANUBIS

Ksenija Poljak

Voditelj: Marin Golub

Zagreb, prosinac 2007.

1. Uvod

Anubis je simetrični algoritam za kriptiranje blokova podataka duljine 128 bitova, a koristi ključ duljine 128, 160, 192, 224, 256, 288, ili 320 bitova. Broj rundi ovisi o ključu i iznosi 12, 13, 14, 15, 16, 17, ili 18. Autori algoritma su: Paulo Barreto i Vincent Rijmen. Razvijen je 2000. godine. Bio je jedan od kandidata za NESSIE (New European Schemes for Signatures, Integrity and Encryption).Nije patentiran i može se slobodno koristiti u bilo koje svrhe.

Anubis je oblik algoritma Rijandael koji koristi involuciju za različite operacije. To omogućava jeftiniju hardware-sku i lakšu software-sku implementaciju algoritma. Postoje dvije verzije Anubisa. Jedna koja koristi klasične S tablice i druga koja ima modificirane S tablice za učinkovitiju hardware-sku izvedbu i ta se naziva ''tweaked'' verzija.

ANUBIS je dobio ime po egipatskom bogu koji je, prema legendi, nadgledao proces mumifikacije, vodio mrtve kroz podzemlje testirajući njihovo znanje o bogovima i njihovu vjeru. Također se smatrao bogom enkripcije, što je i glavni razlog davanja tog imena algoritmu.

2. Opis algoritma

Algoritam je dizajniran prema strategiji širokog repa. Linearni difuzijski sloj osigurava da nakon nekoliko rundi svi izlazni bitovi ovise o svm ulaznim bitovima. Nelinearni sloj osigurava da ta zavisnost bude složene i nelinearne strukture. Jedna od prednosti te strategije je u tome što se pojedine komponente algoritam mogu ostvariti u potpunosti nezavisno jedna o drugoj. Osim u navedenim slojevima, strategija se primjenjuje i u generiranju ključeva.

ANUBIS pripada istoj skupini algoritama kao AES. Osnovne razlike tih dvaju algoritama prikazne su sljedećom tablicom:

Tablica 1: Razlike AES - ANUBIS

Ulazni podatak i svako sljedeće stanje interno su prikazani u obliku matrice 4 x 4 u GF(2⁸) konačnom polju: M_4x4[GF(2⁸)], dok se ključ prikazuje kao N x 4 matrica M_Nx4[GF(2⁸)]. Pretvorba niza bajtova u matrični oblik vrši se funkcijom:

μ : [GF(2⁸)]^4N → [GF(2⁸)]

, a obrnuta operacija njenim inverzom:

2.1. Nelinearni sloj γ

Funkcija nelinearnog sloja γ : M_Nx4[GF(2⁸)] → M_Nx4[GF(2⁸)] sastoji se od nelinearne supstitucije S : [GF(2⁸)] → [GF(2⁸)] , na sve bajtove argumenta individualno:

Supstitucijska talblica S je odabrana na pseudoslučajan način uz sljedeće uvjete:

• S-tablica je involucijska, tj. vrijedi S [ S [ x ] ]=x.

• Parametar δ ne smije nadmašiti vrijednost 8 x 2^-8

• Parametar λ ne smije nadmašiti vrijednost 16 x 2^-6

• Nelinearni red ν mora biti maksimalan, tj. ima vrijednost 7.

Konkretno, izračunato je da S-tablica ima λ =13 x 2^-6 . Eksperimentalno je dokazano da su involucije za δ < 8 x 2^-8 i λ < 13 x 2^-6 veoma rijetke, s obzirom na to da u 600 milijuna slučajno generiranih S-tablica sa danim svojstvima, nije pronađena ni jedna.

Da bi se ubrzao pronalazak odgovarajuće S-tablice, dodani su i sljedeći uvjeti:

• S-tablica ne smije imati ni jedan fiksni element, tj.

• vrijednost svake razlike x ⊕ S[x], mora se pojaviti točno dva puta

2.2. Ispravak S-tablice - “tweak” verzija

Prva verzija S-tablice u sebi sadrži manu. Parametar λ je pogrešno izračunat kao

λ =13 x 2^-6

, dok je zapravo stvarna vrijednost

λ =13 x 2^-6

što je nešto lošije od ograničenja zadanog uvjetima. Zato je uvedena nova struktura S-tablice,koja ne samo da zadovoljava postavljene uvjete, već omogućuje i bolju hardware-sku implementaciju.

Osnovna struktura algoritma time nije promijenjena. S-tablica koja je u originalnoj verziji generirana u potpunosti na slučajan način, zamjenjena je rekurzivnom strukturom. Nova 8 x 8 tablica sastavljena je od manjih, 4 x 4 pseudo-slučajno generiranih tablica kao što je prikazano na slici 1.

Slika 1: Generiranje S-tablice ("tweak")

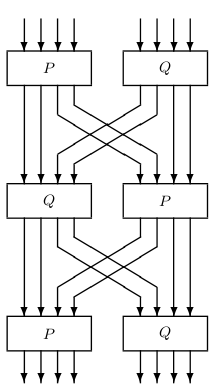
Tablica 2: Mini tablica P

Tablica 3: Mini tablica Q

Nova S-tablica prikazana je na slici2:

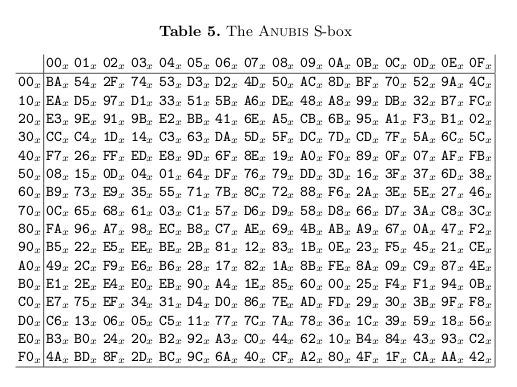
Slika 2: S-tablica

2.3. Transpozicija τ

Funkcija τ: M_4x4[GF(2⁸)] → M_4x4[GF(2⁸)] vrši transpoziciju prema sjedećoj formuli:

τ je očito involucija.

2.4. Linearni difuzijski sloj θ

Difuzijski sloj θ: M_Nx4[GF(2⁸)] → M_Nx4[GF(2⁸)] je nelinearno preslikavanje koje se bazira na [8,4,5] MDS kodu sa matricom generiranja

G_H = [IH],

pri čemu je

H = had('01', '02', '04', '05').

Npr:

tako da vrijedi:

Matrica H je simetrična i unarna, dakle θ je involucija za N=4.

2.5. Dodavanje ključa σ[k]

Funkcija dodavanja ključa σ[k] : M_Nx4[GF(2⁸)] → M_Nx4[GF(2⁸)] zapravo je operacija XOR s matricom ključa M_Nx4[GF(2⁸)]:

Ova funkcija koristi se i za inicijaliziranje konstanti rundi prilikom generiranja ključa. Također je involucija.

2.6. Ciklička permutacija π

Permutacija π: M_Nx4[GF(2⁸)] → M_Nx4[GF(2⁸)] , ciklički posmiče svaki stupac nezavisno, tako da je stupac j posmaknut prema dolje za j pozicija.

2.7. Izvođenje ključa ω

Funkcij izvođenje ključa ω: M_Nx4[GF(2⁸)] → M_4x4[GF(2⁸)] je linearno preslikavanje bazirano na [N+4, N, 5] MDS kodu sa matricom generiranja

G_V=[IV^t]

, pri čemu je

V=vdm_N ('01', '02', '06', '08').

Npr:

tako da vrijedi:

Vandermonde struktura ima sljedeća svojsva:

• Nije teško pronaći MDS Vandermounde matrice nasumičnim pretraživanjem, ukoliko broj redaka nije prevelik.

• Moguće je odabrati Vandermounde matricu sa svojstvima važnim za generiranje podključeva.

• Množenje Vandermounde-ovom matricom može se brzo izvesti pomoću polinomnog algoritma.

2.8. Konstante rundi c^r

Konstanta r-te runde (r>0) je matrica c^r Є M_Nx4[GF(2⁸)]definirana sa:

c^r_0j = S[4 (r-1) + j]

c^r_ij = 0

Valjane konstante ne smiju biti jednake za sve bajtove stanja i moraju biti različite za svaku rundu.

2.9. Proširenje ključa

Ključ K Є GF(2⁸)^4Nproširuje se na četiri podključa

k⁰ = μ(K),

k^r =(σ(c^r) ∘ θ ∘ π ∘ γ)(k^r-1), r>0,

K^r =(τ ∘ ω ∘ γ)(k^r), .

Kompozicija

Ψ = σ(c^r) ∘ θ ∘ π ∘ γ

naziva se key evolution function, a kompozicija

Φ = τ ∘ ω ∘ γ

se naziva key selection function.

2.10. Potpuna definicija ANUBIS-a

ANUBIS je definiran za ključ kriptiranja K Є GF(2⁸)^4N kao transformacija ANUBIS[K] : GF(2⁸)¹⁶ → GF(2⁸)¹⁶ sa:

ANUBIS[K] Ξ μ^-1∘ α_R [K⁰ ,...., K^R] ∘ μ,

gdje je

α_R [K⁰ ,...., K^R] = σ [K^R] ∘ τ ∘ γ ∘ ( σ [K^r] ∘ θ ∘ τ ∘ γ) ∘ σ [K⁰]

Broj rundi R definiran je sa R = 8 + N za 32N-bitni ključ, .

Kompozicija

ρ[K^r] = σ [K^r] ∘ θ ∘ τ ∘ γ

naziva se funkcija runde, a kompozicija

ρ^'[K^R]= σ [K^R] ∘ τ ∘ γ

naziva se zadnja funkcija runde.

3. Otpornost na poznate napade

Prilikom izrade algoritama postavljeni su sljedeći zahtjevi:

Za sve duljine ključa traži se da ANUBIS bude:

• K-siguran – algoritam je K-siguran ako nijedan napad baziran na slabosti generiranja ključa nije brži od prtraživanja cijelog prostora, ako nema istaknute simetrije u funkcijama generiranja ključeva, tj. ako nema poznatih slabosti ključeva.

• Hermetičan – algoritam je hermetičan ako se njegova unutarnja struktura ne može iskoristiti u bilo kojem napadu.

3.1. Diferencijalna i linearna kriptoanaliza

Za bilo koje dvije različite ulazne vrijednosti, broj S-tablica sa različitom ulaznom vrijednišću za četiri uzastopne runde je najmanje

β² = 25.

To ima za posljedicu da ni jedna diferencijalna karakteristika iznad 4 runde nema vjerojatnost veću od

δ^B2 = (2^-5)²⁵

Ni jedna linearna aproksimacija iznad 4 runde, nema ulazno-izlaznu korelaciju veću od

Zbog toga je vjerojatnost uspješnosti napada klasičnom linearnom ili diferencijalnom analizom vrlo malena. Skraćena diferencijalna kriptoanaliza također se pokazala neuspješnom. Za 6 ili više rundi, nije pronađen ni jedan napad brži od pretraživanja potpunog prostora.

3.2. Interpolacijski napad

Uporabom poznatih parova čist tekst – kriptirani tekst, napadač opisujući njihovu relaciju generira polinome. Ukoliko je stupanj polinoma malen, potrebno je samo nekoliko parova. Složenost slučajno odabrane S-tablice u kombinaciji sa difuzijskim slojem, čine ovaj napad nemogućim za više od nekoliko rundi.

3.3. Slabost ključeva

Ova opasnost se javlja kod algoritama kod kojih nelinearne operacije ovise o konkretnim vrijednostima ključa. ANUBIS nema restrikcije na odabir ključa, te su stoga ovakvi napadi neučinkoviti.

Za duljine ključeva veće od duljine jednog ključa runde, neizbježno je da postoji skup ključeva koji generiraju istu vrijednost za barem jedan podključ runde. Za napad pomoču ključeva, značajna je vjerojatnost pronalaska dva različita ključa sa jednakom vrijednošću za dvije uzastopne runde.

Konkretno za ANUBIS, dvije različite k^r vrijednosti mogu proizvesti jednaki ključ rundi K^R samo ako se za sva 4 stupca tablice V razlikuju u ili 0 ili najmanje 5 bajtova. Da bi se proizvela takva dva ključa za dvije uzastopne runde r i r-1, potrebno je da svojstvo bude zadovoljeno za k^r i k^r-1. Difuzojski sloj osigurava da za k^r i k^r-1 barem 5 stupaca mora biti različito. Nema jasne predođbe kako bi takvi ključevi, ukoliko ih je moguće pronaći, mogli omogučiti učinkovit napad.

3.4. Gilbert – Minier napad

Napad probija 7 rundi sa složenošću: 2³² pokušeja na jednan stupac ključa prve runde x 2¹⁶ c-sets x 16 enkripcija po ulazu 2⁸⁰ ulaza/tablici x 2 tablice = 2¹³³ enkrupcija (približno 2¹⁴⁰ pretraživanja S-tablica), plus 2³² odabrana teksta. Prema autoru, postoji ubrzanje za 128-bitovni ključ, čineći napad u tom slučaju minimalno bržim od pretraživanja prostora rješenja.

4. Rezultati ispitivanja efikasnosti

Ovi rezultati odnose se na 550MHz Pentium III platformu.

Postavljanje ključeva kod dekriptiranja rezultira nešto večom potrošnjim nego kod kriptiranja. Dekriptiranje i kriptiranje su podjednako efikasni za svaku veličinu ključa, tj. za svaki moguči broj rundi. To je posljedica svojstva involucije.

5. Zaključak

ANUBIS je zbog svoje strukture otporan na mnoge poznate napade. Najučinkovitiji način pronalaska ključa je pretraživanje prostora rješenja. Isplativost tog postupka ovisi o duljini ključa i iznosi 2^m-1 gdje je m broj bitova ključa.

S obziro na to da ANUBIS ima involucijsku strukturu, kriptiranje i dekriptiranje su jednako unčinkoviti za bilo koji broj rundi. Važnost involucije nije samo u prednostima implementacije, već ima utjecaj na povećanje sigurnosti kriptiranja i dekriptiranja.

Zbog jednostavnih funkcija, korištenja jednostavnih operacija, te zbog minimalnog zauzimanja memorijskog prostora, implemenacija je moguća na različitim arhitekturama i različitim platformama, podjednako u hardware-skoj i software-skoj izvedbi.

6. Literatura

Početak