

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 0 | 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 |
| 1 | 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 |
| 2 | 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 |
| 3 | 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 |
|
|
|
|
|
|

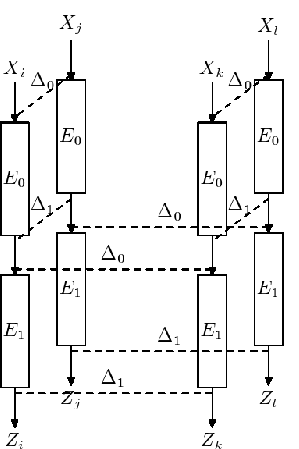
| (4.12) |
|
|
|
|
|
|
|
| broj rundi | pD |
| 3 | [1/234] |
| 5 | [1/55000] |
| 7 | ≈ 2−24 |
| 9 | ≈ 2−32 |
| 11 | ≈ 2−40 |
| 13 | ≈ 2−48 |
| 15 | ≈ 2−56 |
| broj rundi | ND |
| 4 | 24 |
| 6 | 28 |
| 8 | 216 |
| 9 | 226 |
| 10 | 235 |
| 11 | 236 |
| 12 | 243 |
| 13 | 244 |
| 14 | 251 |
| 15 | 252 |
| 16 | 253 |
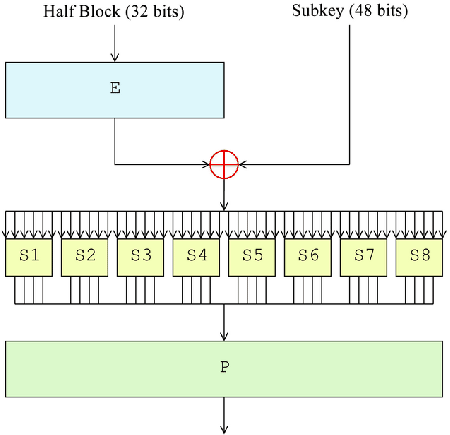
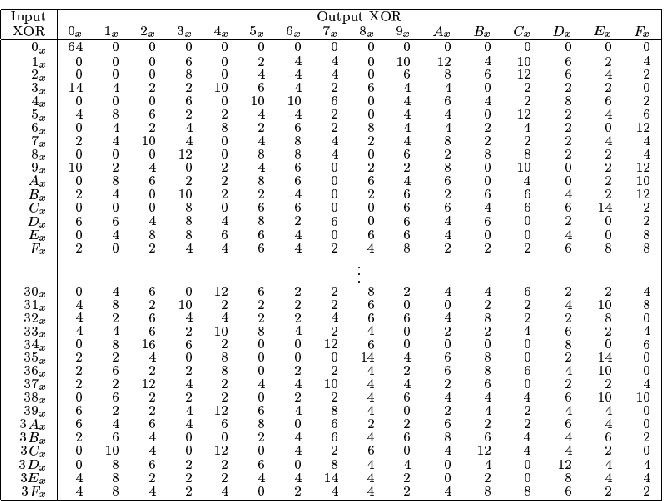
Neka je Sj neka S-kutija (1 ≤ j ≤ 8), te neka je (Bj, B*j) uređeni par 6-bitnih nizova. Tada Bj ⊕B*j se naziva "input XOR", a Sj(B) ⊕Sj(B*j) se naziva "output XOR". Za svaki input XOR (B′j ∈ (Z2)6) skup svih uređenih parova (Bj, B*j) čiji je input XOR jednak B′j je označen sa ∆(B′j).Dakle, ∆(B′j) je u načelu skup od 26=64 uređena para koji sadrže na prvom mjestu sve moguće kombinacije od 6 bita (sve moguće Bj), a na drugom mjestu pripadne 6-bitovne vrijednosti koje sa prvom vrijednošću daju input XOR B′j (dakle, na drugom mjestu se nalazi Bj ⊕B′j):
|
|
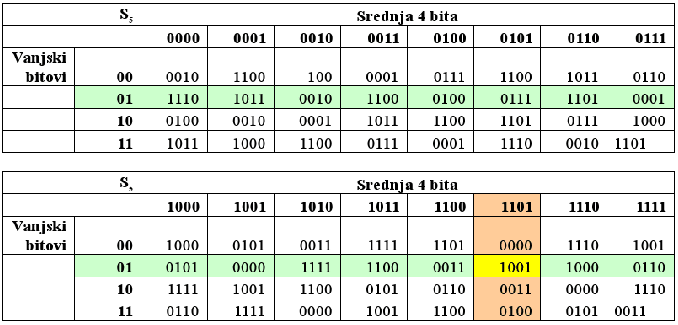
Input XOR: 101010 Raspodjela output XOR-ova: 0000 4 0001 2 0010 4 0011 6 0100 0 0101 2 0110 8 0111 2 1000 2 1001 14 1010 2 1011 6 1100 2 1101 6 1110 2 1111 2 |
Input XOR: 010101 Raspodjela output XOR-ova: 0000 0 0001 4 0010 6 0011 4 0100 2 0101 2 0110 4 0111 10 1000 6 1001 2 1010 0 1011 10 1100 0 1101 4 1110 6 1111 4 |
Input XOR: 110100 Raspodjela output XOR-ova: 0000 0 0001 8 0010 16 0011 6 0100 2 0101 0 0110 0 0111 12 1000 6 1001 0 1010 0 1011 0 1100 0 1101 8 1110 0 1111 6 |
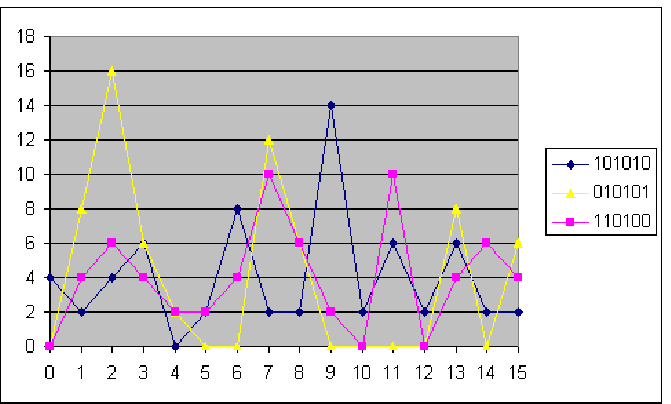
Za j ∈ 1, 2, ... , 8, 6-bitni niz B′j i 4-bitni niz C′j definira se:Matematičkim jezikom ovdje je rečeno da je Nj(B′j, C′j) broj ulaznih parova koji daju input XOR B′j za koje vrijedi da daju output XOR C′j, dok je INj(B′j, C′j) skup 6-bitnih vrijednosti koje čine prvi element ulaznih parova koji čine vrijednost Nj(B′j, C′j). Dakle, Nj(110100, 0001)=8, što je vidljivo iz masno otisnutog retka raspodjele output XOR-ova, dok je
INj(B′j, C′j)
=
Bj ∈ (Z2)6 : Sj(Bj) ⊕Sj(Bj ⊕ B′j) = C′j , (4.27)
Nj(B′j, C′j)
=
| INj (B′j, C′j) |. (4.28)
|
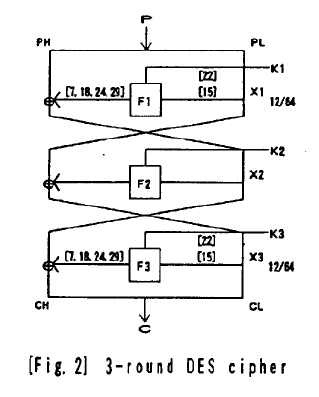
Neka su Ej i E*j 6-bitni nizovi, a C′j 4-bitni niz. VrijediJednostavnim rječnikom rečeno, skup testj dobiva se tako da se izračuna skup INj(Ej ⊕E*j, C′j) te se nad tako dobivenim vrijednostima obavi XOR sa Ej. Obzirom na to da se testj skup gradi nad INj skupom, taj skup isto nasljeđuje svojstvo nejednolike raspodjele vrijednosti na kojoj se temelji diferencijalna kriptoanaliza. Sada je moguće dobiti bitove ključa pomoću test skupova. Ulaz u S-kutiju su 6-bitne vrijednosti koje se dobivaju ekspanzijom 32-bitne vrijednosti na 48-bita, obavljanjem XOR-a te vrijednosti sa 48 bita podključa za tu rundu te rastavljanjem na 8 dijelova od po 6 bita. Analogna situacija postiže se i odvojenim rastavljanjem ekspandirane vrijednosti na 8 dijelova od po 6 bita (označenih sa E1,... E8) te rastavljanjem podključa na 8 dijelova od po 6 bita (označenih sa J1,... J8) i zatim obavljanja XOR-a nad svakim dijelom posebno: Bj=Ej ⊕Jj. Za tako definirane Bj, Ej,Jj vrijedi tvrdnja[12]: Neka je C′j = Sj(Bj) ⊕Sj(B*j). Tada je Jj ∈ testj(Ej, E*j, C′j). Ova tvrdnja izrazito je bitna jer omogućava da se iskoristi činjenica da se vrijednosti skupa test nejednoliko raspoređuju te da se, uz nekoliko parova ulaznih tekstova, odrede presjeci pripadnih skupova test koji sadrže samo jednu vrijednost – traženi dio podključa. Obavi li se ta operacija nad svih 8 dijelova podključa dobiva se cijeli podključ koji daje 48 bitova ključa, što predstavlja razbijanje cijelog algoritma. Slijedi dokaz te tvrdnje: Prema definiciji za testj, tvrdnja koju treba dokazati ekvivalentna je sljedećoj relaciji:
testj(Ej, E*j, C′j) = Bj ⊕Ej : Bj ∈ INj(Ej ⊕E*j, C′j) . (4.30)
|
|
|
|
|
|
|
|
|
|
|
|
|
| Čisti tekstovi: | Kriptirani tekstovi: |
| 3b92ade058430402 | a84d9040984d336b |
| b0461a5858430402 | 5b1c15c8c66ab3c4 |
| c8adf738ab761c20 | aac1c1fb612511d2 |
| d302e329ab761c20 | ee1a40982858724a |
| ef928525e61f62f1 | 90955c3e9e35d6f6 |
| d63da834e61f62f1 | b65a99409ea40565 |
|
|
E1 = 55025bca0201 E*1 = 2f68f80abe50 C′1 = b6f78be2 |
E2 = d55603e03ff7 E*2 = 75c0f42014f1 C′2 = a3862df2 |
E3 = 4a14aaaf81fd E*3 = 5ac2f54f2a01 C′3 = 7904fb6b 2 |
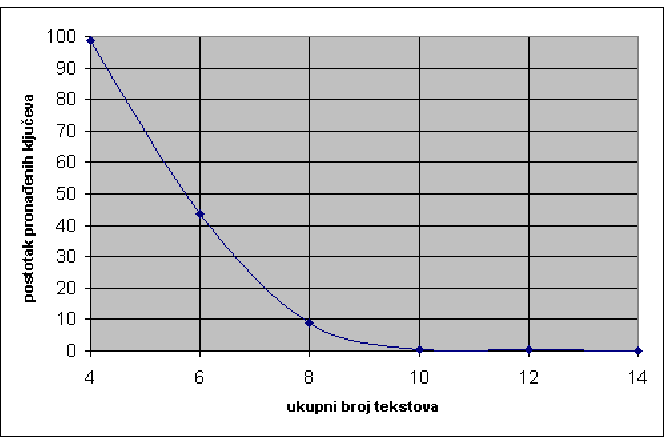
| broj parova čistih tekstova | broj neuspješnih napada |
| 2 | 986 |
| 3 | 435 |
| 4 | 89 |
| 5 | 6 |
| 6 | 4 |
| 7 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
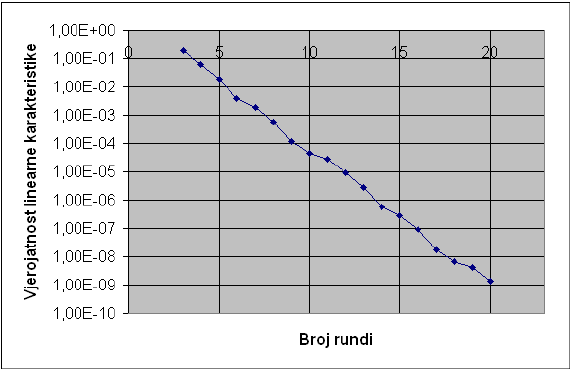
Za n nezavisnih slučajnih binarnih varijabli X1, X2, ..., Xn vrijedi:Ovu lemu može se koristiti za spajanje linearnih karakteristika kroz kriptoalgoritam. Primjerice, ako vrijede sljedeće linearne karakteristike i njihova odstupanja:ili, ekvivalentno:
P(X1 ⊕X2 ⊕... ⊕Xn = 0) = 1/2 +2n−1 n
∏
i=1εi (5.66) gdje ε1,2,...,n predstavlja odstupanje linearne vjerojatnosti za X1 ⊕X2 ⊕... ⊕Xn = 0.
ε1,2,...,n = 2n−1 n
∏
i=1εi (5.67)
|
|
Za danu S-kutiju Sa (a = 1, 2, ..., 8), 1 ≤ α ≤ 63 i 1 ≤ β ≤ 15, definira se NSa(α, β) kao broj setova ulaznih bitova u Sa takvih da je XOR vrijednosti ulaznih bitova maskiranih s α jednaka XOR-u vrijednosti izlaznih bitova maskiranih s β, tj. da vrijedi:
|
|
|
| α/ β | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 4 | -2 | 2 | -2 | 2 | -4 | 0 | 4 | 0 | 2 | -2 | 2 | -2 | 0 | -4 |
| 3 | 0 | -2 | 6 | -2 | -2 | 4 | -4 | 0 | 0 | -2 | 6 | -2 | -2 | 4 | -4 |
| 4 | 2 | -2 | 0 | 0 | 2 | -2 | 0 | 0 | 2 | 2 | 4 | -4 | -2 | -2 | 0 |
| 5 | 2 | 2 | -4 | 0 | 10 | -6 | -4 | 0 | 2 | -10 | 0 | 4 | -2 | 2 | 4 |
| 6 | -2 | -4 | -6 | -2 | -4 | 2 | 0 | 0 | -2 | 0 | -2 | -6 | -8 | 2 | 0 |
| 7 | 2 | 0 | 2 | -2 | 8 | 6 | 0 | -4 | 6 | 0 | -6 | -2 | 0 | -6 | -4 |
|
| N | 2|p − 1/2|−2 | 8|p − 1/2|−2 | 8|p − 1/2|−2 | 16|p − 1/2|−2 |
| Uspjeh | 48,6% | 78,5% | 96,7% | 99,9% |
|
|
|
|
| cijena stroja | predviđeno vrijeme potrage |
| 100.000 $ | 35 sati |
| 1.000.000 $ | 3.5 sati |
| 10.000.000 $ | 21 minuta |
| broj bitova ključa | vrijeme pronalaženja ključa |
| 40 | 78 sekundi |
| 48 | 5 sati |
| 56 | 89 dana |
| 64 | 41 godina |
| 72 | 10.696 godina |
| 80 | 2.738.199 godina |
| 88 | 700.978.948 godina |
| 96 | 179.450.610.898 godina |
| 112 | 11.760.475.235.863.837 godina |
| 128 | 770.734.505.057.572.442.069 godina |

| Vrijeme pronalaska rješenja | Nagrada |
| Manje ili jednako 24 sata | 10.000 $ |
| Više od 24 sata ali manje ili jednako od 48 sati | 5.000 $ |
| Više od 48 sati ali manje ili jednako od 56 sati | 1.000 $ |
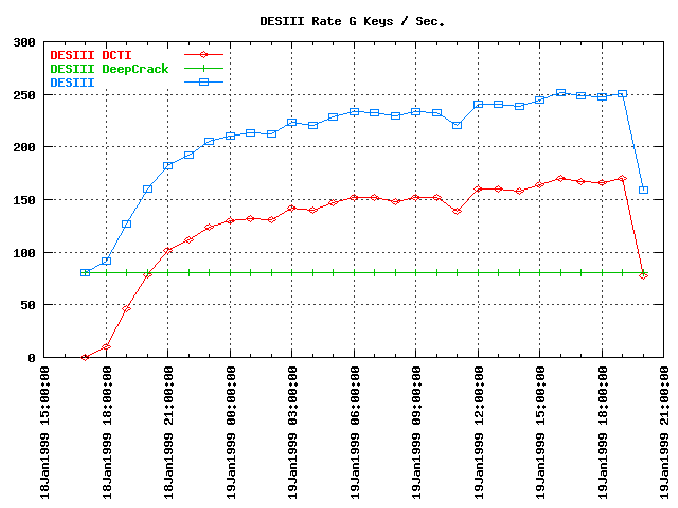


| DES Challenge | Početak natječaja | Vrijeme pretrage | Pretraženo | Najveća brzina pretrage |
| I | 28.1.1997. | 89 dana | 51,8% | 7 * 109 |
| II-1 | 13.1.1998. | 39 dana | 88,4% | 34,4 * 109 |
| II-2 | 13.7.1998. | 56 sati i 3 minute | 24,8% | 90 * 109 |
| III | 18.1.1999. | 22 sata i 15 minuta | 22,2% | 250 * 109 |
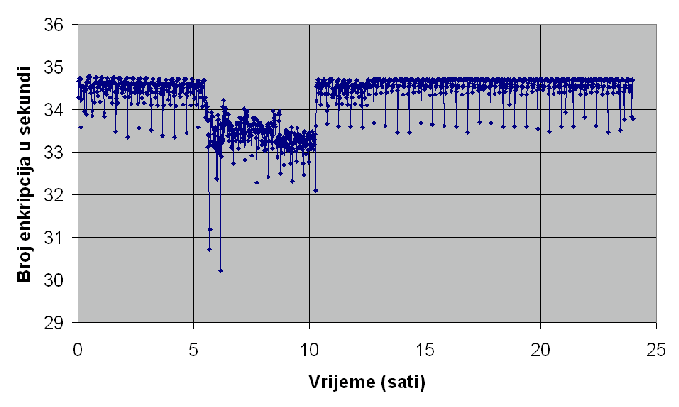
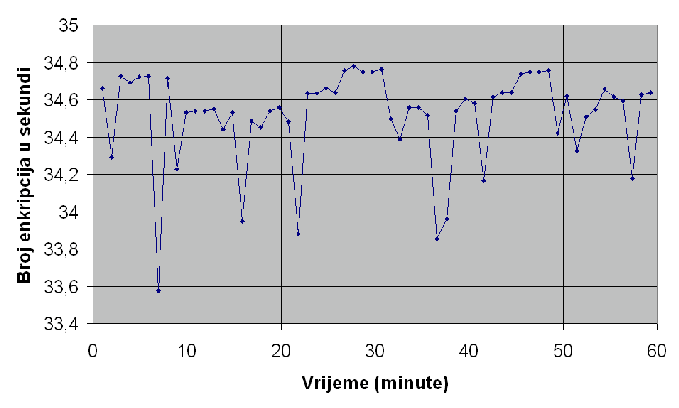
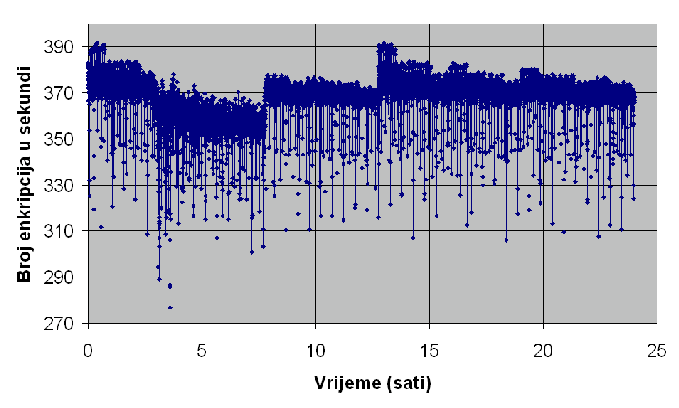
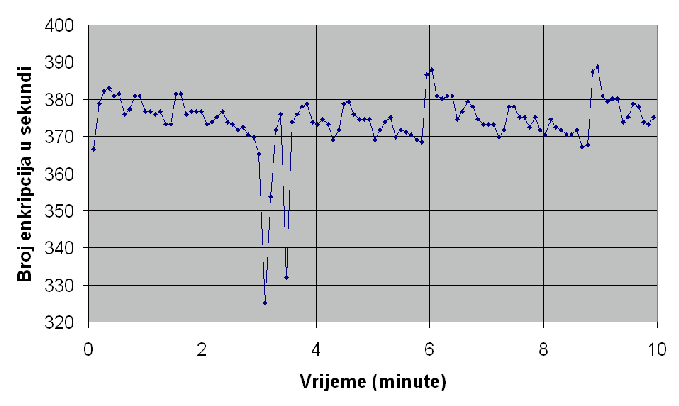
| Implementacija | Prosječno enkripcija u sekundi | Prosječno trajanje napada grubom silom |
| Funkcijska | 34 | 17*109 godina |
| Objektna | 367 | 1,6*109 godina |
| Sklopovska | 2380000 | 246*103 godina |