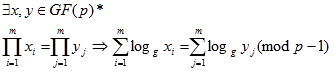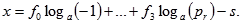Već od samih početaka ljudske civilizacije pojavila se potreba za sigurnom razmjenom poruka između ljudi odnosno ljudskih grupa.
Elementi kriptografije bili su prisutni još u staroj grčkoj stoga ne čudi da je riječ kriptografija grčkog podrijetla te znači
tajnopis. Spartanci su u 5. stoljeću prije Krista koristili kriptosustav zvan skital. Skital se sastojao od štapa na kojem je bila
namotana vrpca pergamenta po kojoj se okomito pisala poruka. Nakon što je poruka bila napisana pergament bi se uklonio s štapa te
bi preostala vrpca s izmiješanim slovima na sebi. Jedini način za pročitati poruku bio je namotavanje vrpce na štap jednake debljine.
Rimski car i vojskovođa Gaj Julije Cezar šifrirao je svoje poruke tako da bi slovo zamijenio onim koje se nalazi 3 mjesta ispred njega
u abecedi uz pretpostavku da je abeceda cikličke naravi. Danas se sve šifre temeljene na ovakvom modelu enkripcije nazivaju Cezarovim
šiframa. Takve šifre se još nazivaju i monoalfabetskim šiframa jer svako slovo ima točno predodređen znak s kojim se zamjenjuje. S
vremenom su nastale i polialfabetske šifre kod kojih se slovo mijenja s nekim od m mogućih znakova ovisno o načinu šifriranja. Primjer
takve šifre je Vigenéreova šifra kod koje se slovo zamjenjuje slovom koje se nalazi k mjesta ispred njega, a k se izračunava kao ostatak
dobiven prilikom dijeljenja pozicije slova u tekstu i ključa m. Daljnji razvoj kriptografije donio je zamjenu blokova slova među prvima
od takvih sistema je Playfairova šifra koja zamjenjuje parove slova. Lester Hill je 1929. Godine osmislio kriptosustav koji je omogućio
zamjenu m slova izvornog teksta s m slova šifrata. Ukoliko duljina teksta nije djeljiva s m potrebno ga je nadopuniti kako bi se provela
podjela na blokove. Potom se konstruira invertibilna matrica m×m. U svakom bloku svakom slovu se odredi njegov numerički ekvivalent koji
je jednak rednom broju slova u abecedi minus jedan. Nakon toga se blok, koji predstavlja vektor s m vrijednosti, množi s matricom m, a u
dobivenom vektoru se dobivene vrijednosti mijenjaju ostatkom njihova dijeljenja s brojem slova u abecedi. Novo dobivene vrijednosti se
prevode u alfabetski oblik. Ovaj način šifriranja naziva se Hillova šifra. Vrijedno je napomenuti da se tokom povijesti nisu svi načini
šifriranja temeljili na supstituciji elemenata izvornog teksta s elementima šifrara. Postojali su i transpozicijski načini šifriranja
čiji je temelj bilo u zamjeni međusobnog položaja elemenata izvornog teksta. Primjer naprave koja je omogućavala ovakvo šifriranje je
Jeffersonov kotač. On se sastojao od 26 pokretnih cilindara s 26 slova na sebi. Jedan od redaka sadržavao je smisleni tekst dok je bilo
koji od preostalih 25 redaka mogao poslužiti kao šifrat. Šifrat bi se poslao osobi s identičnim kotačem koja bi u jednom od redaka
namjestila šifrat i nakon toga među preostalim redcima potražila onaj s smislenom porukom. Tokom drugog svjetskog rata korišteni su
strojevi za kriptiranje ENIGMA i M-209. Enigma se sastojala od tipkovnice s 26 tipki i zaslona od 26 žaruljica, 3 mehanička rotora i
električne prespojne ploče. Pritiskom na tipku upalila bi se žaruljica koja je predstavljala šifrat tog slova. Lako se može primijetiti
kako je siguran prijenos informacija bio izuzetno bitan kroz civiliziranu ljudsku povijest. U današnjem dobu globalizacije informacije
postaju važnije nego ikada prije. Zajedno s njihovim značajem raste i potreba za njihovom sigurnom razmjenom. Iz tog razloga u zadnjih
40-ak godina došlo je do rapidnog razvoja kriptografije[2].
Kriptografija je moderna znanost, bazirana na primijenjenoj matematici, koja se bavi proučavanjem i primjenom tehnika sigurne komunikacije
u prisutnosti treće strane[1][2]. Cilj kriptografije je razvoj i implementacija algoritama čijom primjenom se postiže zadovoljavanje
sigurnosnih zahtijeva:
• Povjerljivost-Informacije u sustavu mogu biti na raspolaganju samo ovlaštenim osobama.
• Raspoloživost-Informacije moraju biti na raspolaganju ovlaštenim osobama bez obzira na okolnosti.
• Besprijekornost-Samo ovlaštene osobe smiju manipulirati podacima
• Autentičnost-Sustav mora biti u stanju jednoznačno prepoznati ovlaštene osobe.
• Autorizacija-Ovlaštenim osobama dopušta se pristup samo do onih informacija koje su im potrebne za obavljanje njihove uloge u sustavu.
• Neporecivost-Korisnici ne mogu opovrgavati svoje akcije u sustavu.
Navedene sigurnosne zahtjeve postavljeni su kako bi spriječili: prisluškivanja, prekidanja, promjene sadržaja informacija, izmišljanja
informacija, lažno predstavljanje te poricanje. Ukoliko dvije sobe razmjenjuju poruke odnosno informacije te se na njihov komunikacijski
kanal to jest put kojim putuje informacija postavi treća osoba koja poruke čita dolazi do prisluškivanja. Ako treća osoba uđe u
komunikacijski kanal ona može prekinuti komunikaciju između prvih dviju osoba, mijenjati sadržaje poruka koje putuju komunikacijskim
kanalom te uspostaviti komunikaciju s jednom od osoba predstavljajući se kao ona druga te tako slati maliciozne poruke. Takve poruke mogu
sadržavati i štetne programe. Zloćudne programe možemo podijeliti u četiri skupine:
• Virusi-programski odsječci koji se infiltriraju u postojeće programe te štetno djeluju.
• Crvi-cjeloviti programi koji djeluju destruktivno.
• Trojanski konj-program koji naočigled obavlja koristan posao, ali sadrži i funkcije štetna djelovanja.
• Rootkiti-programi koji svoje djelovanje skrivaju nadomještajući sustavske procese i podatke.
Kriptiranje omogućuje zadovoljavanje svih sigurnosnih zahtijeva osim raspoloživosti. Kriptiranje je proces sustavnog prevođenja razumljivog
teksta u šifrirani oblik, a dekriptiranje je njemu obrnut proces. Sustavi koji omogućuju kriptiranje nazivaju se kriptosustavi. Kriptosustave
dijelimo u dvije osnovne skupine:
• Simetrični kriptosustavi-za kriptiranje i dekriptiranje koriste jednake ključeve.
• Asimetrični kriptosustavi-za kriptiranje i dekriptiranje koriste različite ključeve.
Glavna odlika simetričnih kriptosustava je korištenje jednog ključa za kriptiranje i dekriptiranje. Korisnici ovakvog sustava moraju prije
komunikacije razmijeniti ključ.
Tablica 2-1 Kriptiranje XOR-om
| Poruka | 1 | 0 | 1 | 1 | 0 | 1 |
| Ključ | 0 | 1 | 1 | 0 | 0 | 1 |
| Kriptirana poruka | 1 | 1 | 0 | 1 | 0 | 0 |
Šifriranje se najčešće provodi primjenom operacije isključivo ili između blokova izvornog teksta i ključa šifriranja, kao što je pokazano u
tablici 2-1 preuzetoj iz [1] Ipak samom primjenom operacije isključivo ili sustav postaje ranjiv na napade "poznavanja izvornog teksta". Ukoliko
je poznat izvorni tekst i njegov kriptirani oblik operacijom isključivo ili između njih dvoje dobiva se ključ šifriranja. Ovaj sigurnosni
rizik moguće je ublažiti tako da se prilikom svakog kriptiranja koristi različiti ključ. Takav način kriptiranja se naziva jednokratnom bilježnicom.
Princip jednokratne bilježnice je nepraktičan jer zahtijeva od korisnika razmjenu teoretski beskonačnog broja ključeva. Kako bi bilo moguće
koristit samo jedan ključ razvijeni su kompleksni algoritmi za kriptiranje[1][2].
2.2 Data Encryption Standard/DES
Data Encryption Standard algoritam osmislio je IBM-ov kriptografski tim 1973. godine. 1976. godine nakon nekih promjena prihvaćen je kao standard[1][2].
Algoritam kriptira poruke u blokovima od 64 bita koristeći 56 bitni ključ K. Izvorni tekst se početno podjeli na blokove od 64 bita. Ukoliko je potrebno
tekst se na kraju nadopuni tako da i posljednji blok bude 64 bitne duljine. Svaki blok se zasebno kriptira primjenom idućih koraka algoritma:
1. Izvorni blok se permutira primjenom specifične inicijalne permutacije IP.
2. Rezultat permutacije se dijeli na lijevi i desni dio, svaki veličine 32 bita.
3. Na dobivene pod-blokove se primjenjuje šesnaest iteracija funkcije transformacije F
1(). Ki su nizovi od 48 bitova koji se dobivaju permutacijom
ključa K.
| F1(Li-1, Di-1)={
Li=Di-1
Di=Li-1 f(Di-1,Ki) ,i e {1,…,16} }
| (2.3) |
4. Konačan šifrat dobiva se primjenom inverzne inicijalne permutacije IP
-1
Lako je primijetiti kako su funkcija f(D
i-1,K
i) i određivanje među-ključeva Ki ključni dijelovi DES algoritma te je potrebno njihovo detaljnije razmatranje.
Računanje među-ključeva obavlja se izvođenjem jednostavnog algoritma, a rezultati se pohranjuju u tablicu ključeva. Originalni ključ K zapravo se sastoji
od 64 bita. Svaki osmi bit je paritetne prirode i postavlja se tako da njegov byte sadrži neparan broj jedinica. Prilikom izvođenja algoritma ovi bitovi se
zanemaruju. Algoritam je moguće podijeliti na tri glavne iteracije:
I. Zanemarujući paritetne bitove ključ se permutira primjenom specifične permutacije PC
1().
II. Rezultat permutacije dijeli se na lijevu i desni dio, svaki veličine 28 bita.
III. Na dobivene pod-blokove se primjenjuje šesnaest iteracija funkcije transformacije F
2() svaka dajući jedan među-ključ kao rezultat.
F2(Ci-1,Ei-1)={
Ci=LSi(Ci-1)
Di=LSi(Di-1)
Ki=PC2(CiDi),
LSi()={"Ciklički pomak lijevo za n mjesta",
i={1,2,9,16, n=1
ostalo, n=2} }
PC2()={"Fiksna kompresijska permutacija"} }
| (2.7) |
Ključevi dobiveni ovim postupkom sudjeluju u izvođenju funkcije f(D
i-1,K
i) koje se sastoji od četiri koraka:
1) Kako bi oba operanda bili jednake duljine D
i-1 se proširuje na 48 bita korištenjem funkcije proširenja E(D
i-1). Funkcija
E(D
i-1) šesnaest bitova duplicira.
2) Nad operandima K
i i E(D
i-1) provodi se funkcija isključivo ili, te na taj način dobiva niz B
i koji se sastoji od osam šest-bitnih pod-nizova
B
i = B
i1… B
i8.
Bi = E(Di-1)
 Ki
Ki | (2.9) |
3) Na dobiveni niz B
i primjenjuje se osam matrica dimenzija 4×16 koje sadrže elemente od 0 do 15,a ih nazivamo S-kutijama. Svaka
se primjenjuje na točno jedan pod-niz. Od šest bitova pod-niza B
ij=b
ij1b
ij2b
ij3b
ij4b
ij5b
ij6 b
ij1b
ij6 određuju binarni zapis
retka matrice, a b
ij2b
ij3b
ij4b
ij5 određuju binarni zapis stupca matrice. Element koji se nalazi na njihovom presjecištu tumačimo
kao binarni broj duljine četiri C
ij te ga uzimamo kao šifru za B
ij.
Cij=Sj-kutija[bij1bij6, bij2bij3bij4bij5],
j={1,…, 8}
Ci=Ci1Ci2Ci4Ci5Ci6Ci7Ci8
| (2.10) |
4) Dobiveni niz bitova C
i=C
i1C
i2C
i4C
i5C
i6C
i7C
i8 duljine je 32-bita. Sada se još na njega primjenjuje konačna permutacija P().
Korištene S
-kutije ne mogu biti bilo kako ispunjene već postoji pet kriterija koji moraju biti zadovoljeni:
i. Svaki redak mora sadržavati sve brojeve od 0 do 15.
ii. Niti jedna S-kutija ne smije biti linearna ili afina funkcija ulaznih podataka.
iii. Promjena jednog bit ulaznog podatka nakon primijene S-kutije rezultira promjenom barem dva bit izlaznog podatka.
iv. Za svaku S-kutiju i svaki ulazni podatak Bij rezultati od S[Bij] i S[Bij  001100]se razlikuju u barem dva bita
v. Za svaku S-kutiju i svaki ulazni podatak Bij i sve e,f e {0, 1} vrijedi S[Bij]
001100]se razlikuju u barem dva bita
v. Za svaku S-kutiju i svaki ulazni podatak Bij i sve e,f e {0, 1} vrijedi S[Bij] 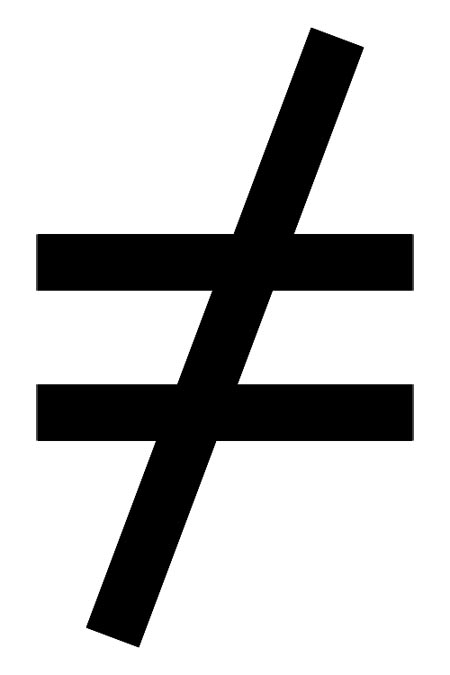 S[Bij
S[Bij  00ef00].
00ef00].
Završna permutacija P() ima zadatak povećanja difuzije kriptosustava te mora zadovoljavati tri kriterija:
- Četiri izlazna bita iz svake S-kutije moraju utjecati na šest različitih S-kutija u idućoj rundi.
- Četiri izlazna bit iz svake S-kutije u i-toj rundi su distribuirana tako da dva od njih utječu na središnje bitove, a dva na krajnje
bitove u (i+1)-voj rundi.
- Za dvije S-kutije Sk i Sj mora vrijediti da ako neki izlazni bit od Sj utječe na neki od središnjih bitova Sk u idućoj rundi, onda niti jedan od izlaznih bitova Sk ne utječe na središnje bitove od Sj.
DES algoritam ima svojstvo da mala promjena ulaznih podataka vuče velike promjene u izlaznim podacima. Ovo svojstvo ponekad se naziva
"efekt lavine" i izuzetno je poželjno u kriptografiji jer povećava otpornost na napade diferencijalnom kriptoanalizom.
Triple Dana Encryption Standard odnosno 3DES nije ništa više nego primjena DES algoritma 3 puta koristeći tri različita ključa K
1, K
2 i K
3.
| 3DES(BLOK,K1, K2,K3)=DES(DES-1(DES(BLOK, K1), K2), K3)
| (2.12) |
Ovako implementiran algoritam omogućuje korištenje 3DES-a poput DES ako se za sva tri ključa odabere identična vrijednost[1][2].
Godine 1997. NIST je raspisao natječaj za razvoj novog enkripcijskog standarda. DES odnosno 3DES naprosto nije zadovoljavao sve zahtjeve
tehnoloških tokova,a i sigurnost DES sustava je postajala upitna. 3DES-u je za kriptiranje potrebno 48 iteracija za postići sigurnost
koja bi se vjerojatno mogla postići u 32 iteracije, 64-bitni blokovi nisu uvijek praktični za rad i prespor je za neke primjene, kao što
je digitalna obrada video signala. Novi algoritam mora je zadovoljavati sljedeće zahtjeve:
• Morao je biti simetričan.
• Mora je kriptirati 128-bitne blokove.
• Mora je raditi s ključevima duljine 128, 192 ili 256 bitova.
• Izvorni tekst algoritma treba je biti javno dostupan.
Pobjednik natječaja bio je Rijandel te tako dobio naziv Advanced Encryption Standard[1][2]. Za potrebe kriptiranja AES koristi konačno Galoisovo polje
oblika GF(2
8) to jest polje konačnog broja elemenata gdje su elementi polinomi oblika a
7x
7+ a
6x
6+ a
5x
5+ a
4x
4+ a
3x
3+ a
2x
2+ a
1x+ a
0, a
i={0,1}. Nad
poljem su definirane operacije zbrajanja i množenja modulo fiksni ireducibilni polinom x
8+ x
4+ x
3+x+1. 8-bitne podatci se prikazuju u obliku
polinoma npr. podatku 10011101 odgovara polinom x
8+ x
5+x
4+ x
3+1. AES kriptira blokove od 128 bitova odnosno 16 bajtova uz pomoć ključa duljine
128 bitova.
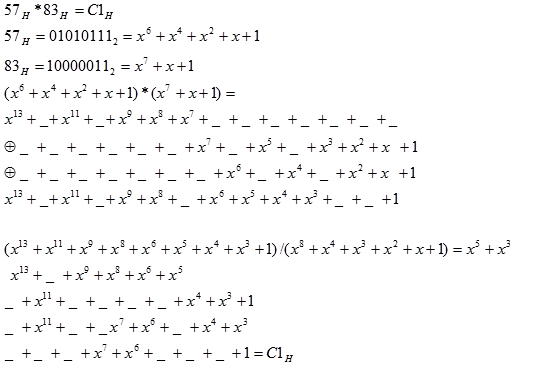 | (2.13) |
Svaki bajt bloka interpretira se kao element 4×4 matrice oblika Galiosova polja. Tu matricu nazivamo AES-blok. Algoritam kriptiranja bloka se odvija
u 10 iteracija, a iteracije se sastoje od 4 dijela:
- Subbytes zamjenjuje svaki element AES-bloka s njegovim GF(28) inverzom te potom na svaki bit bloka primjenjuje fiksu afinu
transformaciju. Transformacijuje moguće prikazati pomoću S-kutije. Prikazujući elemente AES-bloka u heksadecimalnom obliku prvi broj
moguće je tumačiti kao oznaku reda, a drugi kao oznaku stupca S-kutije. Element se zamjenjuje s onim elementom S-kutije koji se nalazi
na presjecištu označenog reda i stupca.
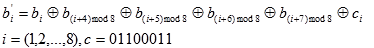 | (2.14) |
- Shiftrows ciklički posmiče redove novo dobivenog bloka ulijevo za i mjesta, gdje je i broj reda nad kojim se vrši operacija.
- Mixcolums miješa stupce AES-bloka. Elementi stupca se tumače kao polinom oblika a3ix3+ a2ix2+ a1ix+ a0i te GF(28)-množe polinomom
03x3+01x2+01x+02. Konačan rezultat dobiva se primjenom modulo x4+1 na rezultat množenja polinoma. U posljednjoj iteraciji miješanje stupaca se izostavlja.
- Addroundkey provodi XOR operaciju nad AES blokom s međuključem odgovarajuće runde. Ovaj korak provodi se dodatno prije prve iteracije.
Konstrukciju međuključeva za posljednji dio algoritma može se podijeliti na dva dijela:
1) Proširenje ključa koje se ostvaruje pomoću XOR-a i cikličkog pomaka. Prva četiri bajta proširenog ključa predstavljaju izvorni
ključ. Daljnji bajtovi ri se konstruiraju kao XOR r
i-1 i r
i-4. Ukoliko se radi o iteraciji u kojoj je i višekratnik od 4 prije XOR-a
se primjenjuje rotacija bajta jedno mjesto ulijevo, na svaki bajt riječi se primjenjuje S-kutija te XOR s riječi [02
(i-4)/4,00,00,00].
Ključ se proširuje do 44 bajta.
2) Iz proširenog ključa međuključevi se biraju tako da prva četiri bajta proširenog ključa predstavljaju prvi međuključ, druga četiri drugi međuključ itd.
Za razliku od DES algoritma kod AES-a su jasno definirana pravila konstrukcija S-kutija. S-kutija se generira određujući multiplikativni
inverz dobivenog broja iz GF(2
8). Cilj S-kutija je što veća otpornost sustava na diferencijalnu i linearnu kriptoanalizu dok miješanje stupaca
i posmak redova služe kako bi povećali difuziju sustava. Dekriptiranje šifranta odvija se na isti način kao i šifriranje izvornog teksta.
Jedina razlika je što se koriste inverzi operacija te se primjenjuju obrnutim redoslijedom. Slika 2-1 grafički prikazuje kriptiranje i
dekriptiranje pomoću AES algoritma. Slika je preuzeta s adrese:
http://www.iis.ee.ethz.ch/~kgf/acacia/fig/aes.png .
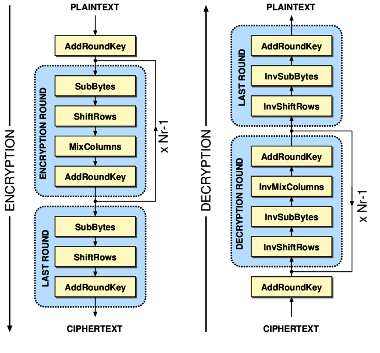 | |
Slika 2-1 AES
Za razliku od simetričnih kriptosustava gdje se kriptiranje i dekriptiranje provodi uz primjenu samo jednog ključa kod asimetričnih
kriptosustava svaki postupak ima svoj ključ. Ovakav način kriptiranja zasniva se na teoriji brojeva te je za njegovo razumijevanje
potrebno poznavanje njenih osnovnih koncepata[1][2][4].
• Djeljivost-a je djeljiv s d ako je a višekratnik od d. Najveći takav d je a, a najmanji 1. Ove djelitelje nazivamo trivijalnim
djeliteljima. Preostali djelitelji se nazivaju faktori broja a.
• Teorem dijeljenja kaže da za svaki cijeli broj a i prirodni broj n postoje brojevi q i r tako da vrijedi: a=q*n+r.
• Ekvivalentnost po modulu tj. kongruentnost brojeva kaže da je broj a kongurentan broju b po modulu n ako vrijedi: a mod n=b mod n.
• Brojevi a i b su relativno prosti ukoliko nemaju zajedničkih faktora.
• Eulerova phi funkcija. Skup Z
n={0,1,…,n-1} je prsten u kojem su definirane operacije zbrajanja, oduzimanja i množenja po modulu n. Z
n*
je podskup od Zn koji se sastoji od elemenata koji su relativno prosti u odnosu na n. Broj takvih elemenata u skupu Z
n* naziva se
njegova kardinalnost i jednaka je Eulerovoj phi tj totient funkciji

(n). Ako je n prosti broj p tada je

(p)=p-1. Ako n nije prosti
broj,
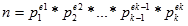
onda vrijedi:
 (n)=n* (n)=n*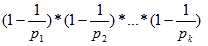 | (3.1) |
Ako n=q*p vrijedi:
 (n)=n* (n)=n*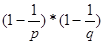 =(p-1)*(q-1) =(p-1)*(q-1) | (3.2) |
• Modularno potenciranje. D=b
a mod n, gdje je a
ma
m-1a
m-2…a
1a
0 binarni prikaz broja a, moguće je izračunati algoritmom:
Ako n=q*p vrijedi:
for(i=m,d=1;i>=0;i--){
d=(d*d)%n;
if(a[i]==1){
d=(d*b)%n;
}}
| (3.3) |
• Eulerov teorem kaže da za svaki prirodni broj n>1 vrijedi:
a (n) mod n =1, za svaki a element od Zn* (n) mod n =1, za svaki a element od Zn*
| (3.4) |
• Mali Fermatov teorem kaže da za proste brojeve p vrijedi:
|
ap-1 mod p=1, za svaki a element od Zn*
| (3.5) |
Što za posljedicu ima:
|
ap mod p=a, za svaki a element od Zp
| (3.6) |
• Ako je a osnovni korijen od Z
n* i b element od od Z
n* postoji x tako da vrijedi:
Broj x se naziva diskretni logaritam tj. indeks broja b (mod n) u odnosu na bazu a.
• Kineski teorem ostatka kaže da za n=n
1* n
2*…* n
k-1* n
k, gdje su svi dvočlani podskupovi faktora relativno prosti, struktura od
Z
n je jednaka Kartezijevu produktu Z
n1* Z
n2*…* Z
nk. U praktičnoj primjeni to znači da za n
1=p i n
2=q za bilo koja dva cijela broja
x i a vrijedi:
x mod p=a
x mod q=a
| (3.8) |
ako i samo ako vrijedi:
Uz pomoć navedenih koncepata teorije brojeva konstruiraju se dva različita ključa, ali ipak matematički povezana. Jedan ključ je javni
i služi za enkripciju izvornog teksta, dok je drugi tajni odnosno privatni. Bilo tko može javnim ključem kriptirati tekst, ali ga samo
osoba s privatnim ključem može lakoćom dekriptirati, bilo kome drugom bilo bi potrebno ulaganje neisplativo velikih napora. To je osnovni
koncept asimetrične kriptografije.
Sigurnosni algoritam RSA razvijen je 1977. godine[1][2]. Ime je dobio kao kombinaciju imena svojih tvoraca. Algoritam se zasniva na teškoći
faktorizacije velikih prirodnih brojeva iako se tokom samog kriptiranja i dekriptiranja koristi modularno potenciranje. RSA kriptosustav
definiran je kao:
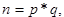 gdje su p i q prosti brojevi gdje su p i q prosti brojevi
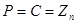 te vrijedi: te vrijedi:
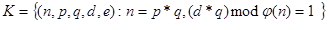
Za i e :
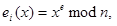 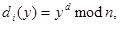 x,y e Zn x,y e Zn
| (3.10) |
Vrijednosti n i e su javni ključ, a vrijednosti p,q i d su tajni ključ.
Funkcije e
i(x) i d
i(y) su međusobno inverzne tj. e
i(d
i(x))=x. Provođenje RSA algoritma može
se podijeliti u 3 dijela.
- Generacija ključeva. Odabiru se dva velika prosta broja p i q, tako da je p,q>10150. Brojevi p i q ne smiju biti sličnih vrijednosti
jer to olakšava njihovo određivanje. Isto tako je poželjno da p
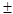 1 i q
1 i q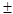 1 sadrže barem jedan veliki prosti faktor jer postoje efikasne metode
faktoriziranja brojeva koji sadrže samo male proste faktore. Nakon određivanja p i q izračunava n=p*q, a potom
1 sadrže barem jedan veliki prosti faktor jer postoje efikasne metode
faktoriziranja brojeva koji sadrže samo male proste faktore. Nakon određivanja p i q izračunava n=p*q, a potom  (n). Odabire se broj e<
(n). Odabire se broj e< (n),
takav da je relativno prost u odnosu na
(n),
takav da je relativno prost u odnosu na  (n). Uz pomoć e i
(n). Uz pomoć e i  (n) se izračunava d, tako da vrijedi:
(n) se izračunava d, tako da vrijedi:
e*d mod  (n)= 1 (n)= 1
| (3.11) |
- Šifriranje. Poruka x < n se kriptira javnim ključem.
- Dešifriranje. Šifrant y se dekriptira privatnim ključem.
 | |
Slika 3-1 RSA
Slika 3-1 prikazuje osnovne korake prilikom generacije ključa, enkripcije i deskripcije pomoću RSA algoritma, a preuzeta je s adrese:
http://www.arl.wustl.edu/~jl1/education/cs502/course_project.htm Za efikasnost RSA sustava važne su činjenice da je faktorizacija
brojeva od već 1024-bita neizvediva u razumnom vremenu, a modularno potenciranje veoma efikasno izvedivo uz pomoć prethodno navedenog
algoritma. Razlika složenosti navedenih postupaka ključ je uspjeha RSA algoritma.
Kriptografija pomoću eliptičnih krivulja ušla je u masovnu uporabu 2004. godine. Ovaj tip kriptografije bazira se na algebarskoj
strukturi eliptičnih krivulja u konačnim poljima[2][6]. Za razliku od RSA sustava koji svoju sigurnost bazira na problemu faktorizacije
velikih prirodnih brojeve kod eliptičnih krivulja sigurnost je bazirana na problemu nalaženja diskretnog logaritma nasumičnog elementa
eliptične krivulje. Za trenutne kriptografske potrebe uzima se eliptična krivulja čiji elementi zadovoljavaju jednadžbu[3.14], zvanu
kratka Weierstrassova formula, zajedno s točkom u beskonačnosti, a one su definirane nad poljem K karakteristike različite od dva ili tri:
y2=x3+ax+b
a,b e K
| (3.14) |
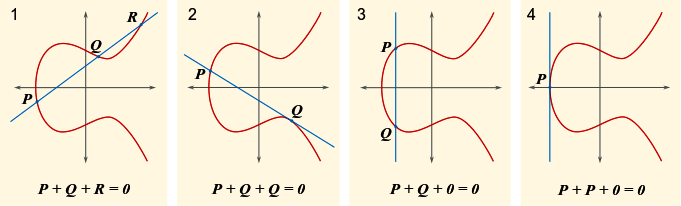 | |
Slika 3-2 Operacije nad eliptičnim krivuljama
Navedeni polinom ne smije imati višestruke korijene. Važno svojstvo eliptičnih krivulja je da se nad njima mogu definirati operacije uz
koje one postaju Abelove grupe. Operacije nad eliptičnim krivuljama ilustrirane su na slici 3-2 koja je preuzeta s adrese:
http://en.wikipedia.
org/wiki/Elliptic_curve .Glavna prednost ECC kriptografije je manja veličina ključa čime se smanjuju memorijske potrebe te povećava
brzina prijenosa. Odnos veličina ključeva prilikom primjene ECC kriptografije,RSA algoritma i AES algoritma prikazan je na slici 3-3 koja
je preuzeta s adrese:
http://www.embedded.com/design/connectivity/4025631/Understanding-elliptic-curve-cryptography . 256-bitni ECC ključ
pruža sigurnost ekvivalentnu 3072-bitnom RSA ključu. Najčešće korišteni ECC algoritmi današnjice su:ECDH, ECES, MQV i Menezes-Vanstone.
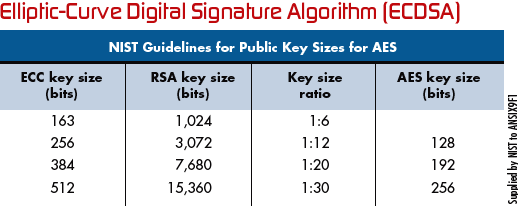 | |
Slika 3-3 Veličine ključeva jednake sigurnosne razine
Funkcije sažimanja/ hash funkcije ulazni niz podataka transformiraju u bitovni niz fiksne duljine tako da i najmanje promjene u ulaznom
nizu gotovo u potpunosti mijenjaju izlazni bitovni niz[1][2][3]. Izlazni nizovi najčešće se prikazuju u heksadecimalnom obliku. Idealne
hash funkcije zadovoljavaju četiri glavna uvjeta:
• Lako je generirati hash tj. izlazni bitovni niz, za svaku poruku bez obzira na njenu duljinu.
• Nemoguće je u razumnom vremenu iz hash-a generirati izvornu poruku.
• Nemoguće je promijeniti poruku bez da se promijeni hash.
• Nemoguće je u naći dvije poruke koje imaju isti hash.
Njihove primjene zalaze i van područja računalne sigurnosti pa su tako često korištene za uspoređivanje i brzo pretraživanje. U kriptografiji
hash funkcije se najviše koriste za potrebe digitalnih potpisa i autentifikacije. Slika 4-1 pokazuje osnovnu ideju rada hash funkcije, a
preuzeta je s adrese:
http://en.wikipedia.org/wiki/Cryptographic_hash_function
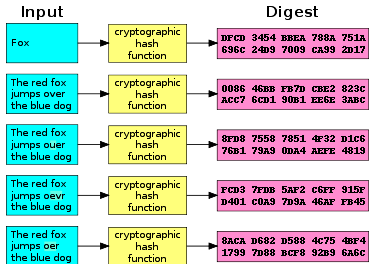 | |
Slika 4-1 Rad hash funkcije
Sigurnosni hash algoritam tj. SHA-2 je zapravo naziv za nekoliko algoritama: SHA-224,SHA-256, SHA-384, SHA-512, SHA-512/256 [2][3].
Njihove oznake označavaju duljine njihovih hash-eva. Algoritam je napravila Američka nacionalna sigurnosna agencija 2001. godine
nakon što je otkriven sigurnosni propust u njegovom prethodniku SHA-1. Navedeni SHA-2 algoritmi međusobno se malo razlikuju stoga
je za razumijevanje njihova rada dovoljna analiza jednog od njih, npr. SHA-256. Izvođenje SHA-256 algoritma moguće je podijeliti
u sedam dijelova:
1. Prvo se inicijalizira 8 hash vrijednosti, h0 do h7. Inicijalizacije predstavljaju frakcionalne dijelove drugih korijena prvih
osam prostih brojeva.
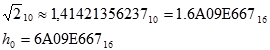
| (4.1) |
2. Inicijalizira se polje od 64 cjelobrojnih konstanti, k
0 do k
63. Konstante se izračunavaju kao frakcionalni dijelovi trećih krojena
prvih 64 prosta broja.
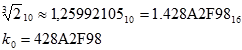
| (4.2) |
3. Tekstu na koji će biti primijenjen hash se dodaje bit 1 te n bitova 0 tako da duljina ukupne poruke pri dijeljenju s 512 daje ostatak
448. Potom se poruci dodaje 64-bitovni zapis koji izražava duljinu poruke bez prethodno dodanih bitova. Na ovaj način dobiva se poruka
čija je duljina cjelobrojni višekratnik od 512.
4. Poruka se dijeli na 512-bitne blokove. Za svaki blok se alocira polje od 64 32-bitne riječi. Blok se upisuje u prvih šesnaest elemenata
polja te potom proširuje u preostalih 48 elemenata polja sljedećim algoritmom:
for(i=16;i<64;i++){
s0= rotiraj_x_u_desno_za_n(w[i-15],7) ^
rotiraj_x_u_desno_za_n(w[i 15] ,18) ^
shiftaj_x_u_desno_za_n(w[i-15],3);
s1=rotiraj_x_u_desno_za_n(w[i-2],17) ^
rotiraj_x_u_desno_za_n(w[i-2],19)^
shiftaj_x_u_desno_za_n(w[i-2],10);
w[i]=w[i-16]+s0+w[i-7]+s1;
}
| (4.3) |
5. Nad rezultatom prethodnog koraka se potom provodi kompresijska funkcija:
for(i=0;i<64;i++){
S1=rotiraj_x_u_desno_za_n(h[4],6)^ rotiraj_x_u_desno_za_n(h[4],11)
^ rotiraj_x_u_desno_za_n(h[4],25);
ch= (h[4] & h[5] ) ^ (~h[4] & h[6]);
temp1= h[7] +S1+ch+k[i]+w[i];
S0=rotiraj_x_u_desno_za_n(h[0],2)^ rotiraj_x_u_desno_za_n(h[0],13)^
rotiraj_x_u_desno_za_n(h[0],22);
maj=(h[0] & h[1] ) ^ (h[0] & h[2] ) ^ (h[1] & h[2] );
temp2=S0+maj;
h[7]= h[6];
h[6]= h[5];
h[5]= h[4];
h[4]= h[3]+temp1;
h[3]= h[2];
h[2]= h[1];
h[1]= h[0];
h[0]=temp1+temp2;
} // h[i]= copy_of(hi) ; k[i]= ki;
| (4.4) |
6. Nakon kompresijske funkcije se originalnim hash vrijednostima h
0,…, h
7 pridodaju izračunate hash vrijednosti h[0],…, h[7]. Tako
da je hi= h[i]+h
i, i e {1,…7}.
7. Konačna hash vrijednost dobiva se spajanjem hash vrijednosti.
|
HASH= h0h1h2h3h4h5h6h7 ;
| (4.5) |
SHA-224 razlikuje se od SHA-265 utoliko što su inicijalne vrijednosti hash-a h
0,…,h
7 drugačije te se na kraju zanemaruje h
7. U ovom
slučaju se za inicijalne vrijednosti uzimaju drugih 32-bita decimalnog dijela drugog korijena od devetog do šesnaestog prostog broja.
SHA-512 radi s 1024-bitnim blokovima, inicijalne hash vrijednosti h
0,…,h
7, cjelobrojne konstante, kojih ovdje ima 80, k
0,…, k
79 i
riječi w
0,…,w
79 prikazuju se s 64-bitnom preciznošću, kompresijska funkcija ima 80 iteracija te koristi drugačije iznose pomaka te
prilikom dodavanja duljine poruke duljina se prikazuje u 128-bitnoj preciznosti.
SHA-384 radi poput SHA-512 uz razliku inicijalnih vrijednosti hash-a te na kraju zanemaruje h
6 i h
7. Za inicijalne vrijednosti hash-a
uzimaju se decimalni dijelovi drugih korijena od devetog do šesnaestog prostog broja.
SHA-512/256 radi poput SHA-512 samo što inicijalne vrijednosti hash-a generira funkcija SHA-512/t IV generation. Izlazni hash se skraćuje
na 256-bita odbacivanjem hash-ev h
4, h
5, h
6 i h
7. Slika 4-2 prikazuje rad SHA-2 algoritma, a preuzeta je s adrese:
http://j-7system.blog.so
-net.ne.jp/2014-01-14 .
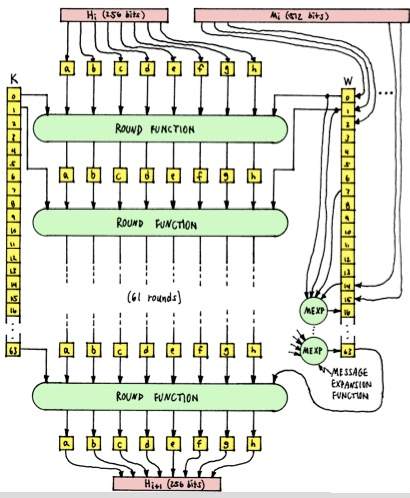 | |
Slika 4-2 SHA-2 algoritam
Iako SHA-2 algoritam pruža adekvatnu sigurnosnu zaštitu postoje teorijski rizici. Iz tog razloga je Američki nacionalni institut za
standarde i tehnologiju 2007. godine raspisao natječaj za razvoj novog hash algoritma. 2012. godine kao pobjednik natječaja objavljen
je Keccak algoritam te je tako postao SHA-3.[3][5][7] Važno je napomenuti da SHA-3 nije razvijeni odnosno unaprijeđeni SHA-2 algoritam.
SHA-3 koristi spužvastu funkciju za obradu podataka. Spužvaste funkcije su algoritmi s konačnim brojem stanja koji obrađuju nizove
proizvoljne konačne duljine te generiraju nizove proizvoljne konačne duljine. Spužvaste se funkcije sastoje od tri dijela:
1. Memorije stanja, S koja se sastoji od b bitova. Bitove memorije stanja moguće je logički podijeliti u dvije skupine. Na bitove
bitrata R i bitove kapacitet C.
2. Funkcije f(S) koja permutira memoriju stanja.
3. Funkciju proširenja P(x), gdje je x ulazni tekst. Funkcija izvorni tekst proširuje tako da njegova duljina postane cjelobrojni
višekratnik bitrata R.
Izvođenje spužvastih funkcija moguće je podijeliti u tri koraka:
I. U prvom koraku inicijalizira se početno stanje S u nula i izvorni tekst se proširuje uz pomoć funkcije P(x).
II. Drugi korak ima onoliko iteracija koliko puta je izvorni tekst veći od bitrata R. Za svaki blok veličine bitrata bitrat i taj blok
se XOR-aju i izvede se Si=f(Si-1).
III. U zadnjem koraku dolazi do ispisa. Bitrat memorije stanja se ispisuje. Ako je traženo još bitova za ispis odvija se Si=f(Si-1)
i nakon toga se bitrat ponovo ispisuje. Ukoliko tražena duljina izlaznog niza nije višekratnik duljine bitrata prilikom zadnjeg ispisa
odbacuju se bitovi viška.
Prilikom izvođenja C dio memorije stanja tj. kapacitetni bitovi se mijenjaju ovisno o funkciji f(S). Kada se spužvaste funkcije koriste
za hash otpornost hash-a na kolizije i otpornost na izračunavanje originala ovise o veličini kapaciteta C. SHA-3 algoritam prilikom
proširenja ulaznog teksta dodaje jednu jedinicu, potom odgovarajući broj nula i na kraju još jednu jedinicu. Algoritam radi s 64-bitnim
riječima stoga se njegova memorija stanja prikazuje kao matrica dimenzija 5*5*64. f(S) funkcija SHA-3 algoritma, zvana još i Keccak
f-permutacijom sastoji se od pet pod-operacija koje se izvršavaju u 24 iteracije, a označavaju se s
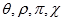
i
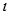
.
1) 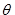 funkcija, prikazana slikom 4-3 preuzetoj iz [5] izračunava paritet svakog stupa matrice te nad svakim elementom matrice provodi
XOR s XOR-om pariteta dvaju predodređenih stupaca. Matematički je funkciju moguće zapisati kao:
funkcija, prikazana slikom 4-3 preuzetoj iz [5] izračunava paritet svakog stupa matrice te nad svakim elementom matrice provodi
XOR s XOR-om pariteta dvaju predodređenih stupaca. Matematički je funkciju moguće zapisati kao:
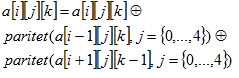
| (4.6) |
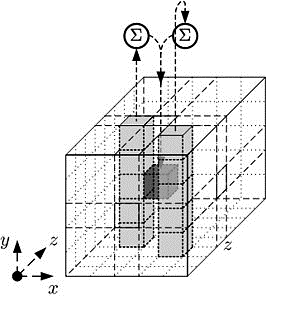 | |
Slika 4-3 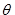 funkcija
funkcija
2)
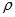
funkcija rotira svaku od 64-bitnih riječi za različiti trokutasti broj mjesta. Rad funkcije prikazan je na slici 4-4 preuzetoj
iz
[5] . Trokutasti brojevi su brojevi oblika Br=
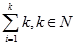
Matematički je postupak funkcije moguće zapisati kao:
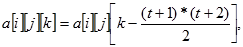 za t=0,…,24 i za t=0,…,24 i 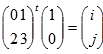
| (4.7) |
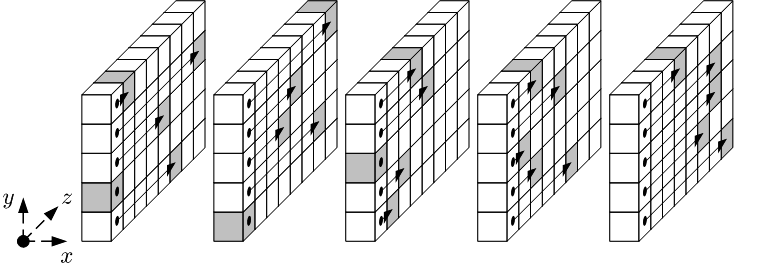 | |
Slika 4-4 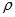 funkcija
funkcija
3)
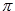
je transpozicija stanja.
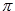
funkcija prikazana je na slici 4-5 preuzetoj iz
[5] Matematički ju je moguće zapisati kao:
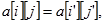 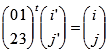
| (4.8) |
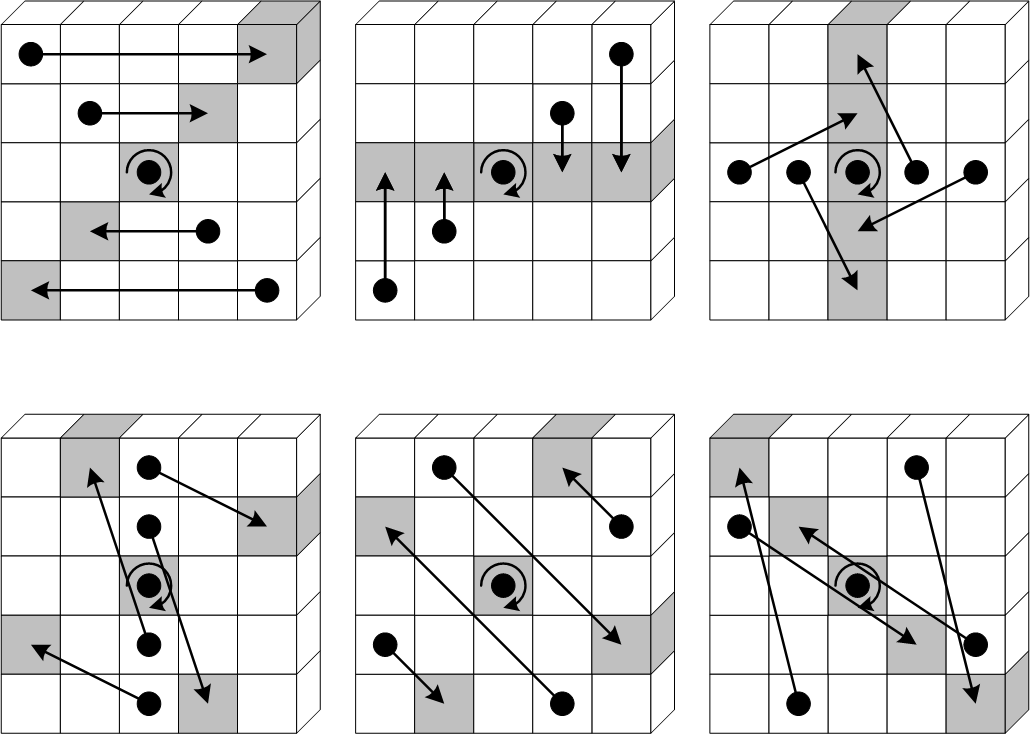 | |
Slika 4-5 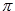 funkcija
funkcija
4)
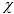
je jedina nelinearna operacija u SHA-3. Svaki element matrice XOR-a se s XOR-om pariteta dvaju predodređenih redova kao što je
prikazano na slici 4-6 preuzetoj iz
[5] . Matematički je operaciju moguće prikazati kao:
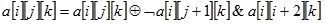
| (4.9) |
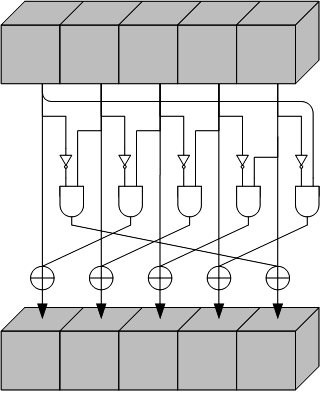 | |
Slika 4-6 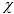 funkcija
funkcija
5)
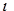
operacija svaki element XOR-a s konstantnom vrijednošću RC[z
r]. Matematički se prikazuje kao:
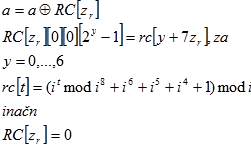
| (4.10) |
Prilikom ispisa SHA-3 duljina dobivenog hash-a je uvijek manja od duljine ulaznog bloka i čitavi izlazni niz se generira u jednoj iteraciji.
Slika 4-7 prikazuje osnovnu ideju rada spužvaste funkcije, a preuzeta je s adrese:
http://os2.zemris.fer.hr/algoritmi/hash/sha3/2013_kraljevic/keccak.html .
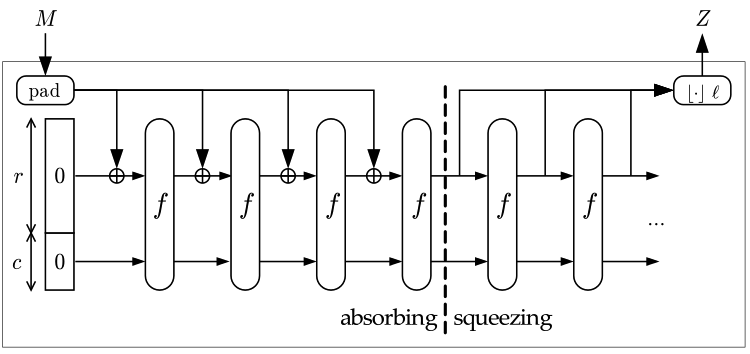 | |
Slika 4-7 Spužvasta funkcija
Kriptoanaliza je znanost koja se bavi analizom sigurnosti kriptografskih algoritama[1][2][3][7]. Znanja kriptoanalize često bivaju
korištena u pokušajima ugrožavanja sigurnosti. Jedna od osnovnih pretpostavki kriptoanalize, zvana Shannon-ova pretpostavka, nalaže
da napadač poznaje sustav odnosno da je algoritam kriptiranja poznat. Ovisno o količini informacija kojom napadač raspolaže moguće
je napraviti podjelu u kriptoanalizi.
• Poznavanje samo šifranta.
• Poznavanje izvornog teksta i njemu odgovarajućeg šifranta.
• Poznavanje točno određenog izvornog teksta i njegovog šifranta.
• Poznavanje više šifranata izvornog teksta koji se razlikuju zbog korištenja različitog ključa kriptiranja. Iako su sami ključevi
kriptiranja nepoznati napadač zna za nekakav logički odnos među njima.
Napade na sigurnosni sustav moguće je dijeliti i s obzirom na resurse potrebne za njihovo izvođenje. Osnovni resursi su:
• Vrijeme. Zbog različitih brzina i načina izvođenja algoritama na različitim procesorima za vrijeme se ne uzima mjera sekunde već
broj osnovnih operacija procesora koje je potrebno izvesti prilikom izvođenja algoritma.
• Memorija. Različiti napadi zahtijevaju različite količine memorijskog prostora za svoje izvođenje.
• Informacije. Različiti napadi zahtijevaju različite količine informacija o sustavu kojeg nastoje ugroziti. Za količinu potrebnih
informacija često se uzima količina izvornog teksta i količina šifranta potrebna za ugrožavanje sustava.
Svaki sustav kriptiranja moguće je probiti primjenom grube sile odnosno isprobavanjem svih mogućih kombinacija. Takav napad često nije
od praktične koristi jer ga je nemoguće izvesti u realnom vremenu. U akademskim krugovima probijanje sustava definira se kao bilo koji
uspješan napad niže složenosti od napada primjenom grube sile tj. brute force napada. Ipak nije ni svaki takav napad od praktične koristi.
Ukoliko napad zahtjeva nerazumne količine vremena, memorije i/ili informacija mogućnost njegova stvarnog izvođenja je nikakva. Probijanja
sustava moguće je podijeliti s obzirom na količinu informacija dobivenih probojem
• Totalnim probojem- slučaj kada napadač otkrije tajni ključ šifriranja.
• Globalnom dedukcijom- slučaj kada napadač sazna funkcijski ekvivalent algoritma ali ne sazna tajni ključ korišten prilikom šifriranja.
• Lokalnom dedukcijom- slučaj kada napadač otkrije dodatne količine izvornog teksta i/ili šifranta.
• Informacijska dedukcija- napadač sazna Shannonovske informacije o izvornom tekstu i/ili šifrantu.
• Prepoznavanje algoritma- napadač prepozna način šifriranja.
Prilikom testiranja sigurnosti sustava proboji se pokušavaju ostvariti na oslabljenim inačicama sustava. Takve inačice često su originalni
algoritmi s pokojom uklonjenom iteracijom. Ovakva testiranja predvidjela su probijanje kriptografskih algoritam DES, MD5 i SHA-1. Obične
zamjenske šifre često je moguće ugroziti frekvencijskom analizom. U prirodnim jezicima određena slova i nakupine slova pojavljuje se učestalije
od drugih. Ukoliko šifrant ne prikriva takve statističke odnose moguće je s određenom dozom sigurnosti pretpostaviti značenja pojedinih dijelova
šifranta te pomoću toga probiti šifru. Ukoliko se više poruka kriptira koristeći jednake ključeve smanjuje se sigurnost kriptiranja. Poznavanje
više poruka istog ključa kriptiranja povećava mogućnost otkrivanja tajnog ključa, a ukoliko se otkrije više takvih ključeva povećava se mogućnost
razotkrivanja principa generiranja ključeva. Za različite kriptografske postupke primjenjuju se različiti kripto-analitički algoritmi. Za simetrične
kriptografske algoritme najčešće se primjenjuju diferencijalna i linearna kriptoanaliza. Probijanje asimetričnih algoritama svodi se na rješavanje
kompleksnih matematičkih problema kao što su faktorizacija velikih prirodnih brojeva i određivanje diskretnih algoritama. Hash algoritmi se mogu
ugroziti s Rođendanskim napadom i Rainbow table algoritmom.
Metode kriptoanalize simetričnih algoritama međusobno se dosta razlikuju. Unatoč tome sve one zasnivaju se na ideji pronalaženja pravilnosti
prilikom kriptiranja koje bi otkrile dodatne informacije o postupku enkripcije. Dekriptiranje ključa ili među-ključa glavni je cilj simetrične
kriptoanalize. Jednom kad je ključ poznat šifrant se jednostavno dekriptira te se dobije izvorni tekst. Linearna, diferencijalna i MITM
kriptoanaliza često su primjenjivane metode kriptoanalize simetričnih blokovskih kriptosustava [7].
Iako su diferencijalnu analizu prvi javno opisali Eli Biham i Adi Shamir 1990. godine postoje indikacije da je postupak bio poznat IBM-ovom
DES timu još 1974. godine te su vodili računa o njemu prilikom konstrukcije S-kutija i P permutacije[2][7]. Po postupku diferencijalna kriptoanaliza
spada u skupinu poznavanja određenog izvornog teksta i njegova šifranta iako postoje verzije koje u nekih algoritama omogućuju napad poznavanjem
samo izvornog teksta ili samo šifranta. Ideja diferencijalne kriptoanalize je usporedba XOR-a dvaju izvornih tekstova L
0R
0, L
0*R
0* i njihovih šifranata
nastalih istim ključem. XOR izvornih tekstova
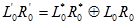
naziva se input tj. ulazni XOR, a šifranata output tj. izlazni XOR, a zajedno čine diferencijal.
Na primjeru DES algoritma moguće je sagledati ideju postupka diferencijalne kriptoanalize te ju razložiti u tri koraka:
1. S-kutija označava se s Sj, j e {1, …, 8}. Par 6-bitnih ulaznih nizova u S-kutiju označava se s Bj, Bj* a par 4-bitnih izlaznih nizova s Sj(Bj) i Sj(Bj*) .
Za svaki par ulaznih nizova jednakog input XOR-a izračunava se output XOR njihovih šifranata. Zbog šest bitova za svaki input XOR postoji
26=64 para. Činjenica da output XOR-ovi nisu uniformno distribuirani između 16 mogućih vrijednosti osnova je diferencijalna napada.
2. Za 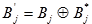 i Cj definira se :
i Cj definira se :
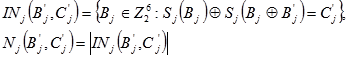
| (5.1) |
Podsjetimo se da vrijedi B
i= E(D
i-1)

K
i za ulazni podatak S-kutije u i-toj rundi. Zbog provedenih operacija vrijedi:
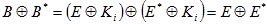
| (5.2) |
Važno je primijetiti kako input XOR ne ovisi o međuključu.
3. B, E, B
*, E
*, K zapisuju se kao:
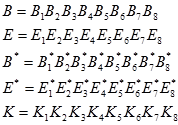
| (5.3) |
Potom se definira:
Za navedeni skup jednadžbi vrijedi:
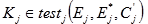
| (5.5) |
Primjenom ovog algoritma dobiva se međuključ što znatno olakšava postupak određivanja cjelokupnog ključa.
Linearna kriptoanaliza je napad poznavanjem izvornog teksta i njegova šifranta [2][7]. Ona se zasniva na ideji da iako bitovi ključa
nisu linearne funkcije neki od njih mogu se dobro aproksimirati linearnim funkcijama. Postupak linearne kriptoanalize moguće je razložiti
na sljedeći način:
I. Bitovi izvornog teksta, šifranta i ključa označavaju se kao:
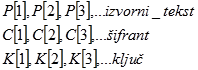
| (5.6) |
Uvodi se i oznaka:
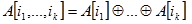
| (5.7) |
II. Nakon toga traže se linearne jednadžbe oblika:
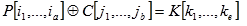
| (5.8) |
koje za nasumični izvorni tekst i šifrant vrijede s vjerojatnošću
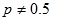
. Vjerojatnost desne strane dobiva se njenim izračunavanjem za veliki
broj parova izvorni tekst, šifrant.
III. Ako je u više od pola slučajeva na lijevoj strani nula i
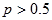
za vrijednost se uzima nula, a za
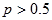
se uzima jedan. Na taj način dobiva
se linearna jednadžba u bitovima ključa. Uz dovoljno velik broj takvih jednadžbi postaje moguće odrediti ključ.
IV. Kako bi metoda bila uspješna kod DES algoritma preporuča se uzimanje
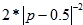
parova izvornog teksta i šifranta.
Linearnu kriptoanalizu prvi je opisao Mitsuru Matsui 1993. godine kao teoretski napad na DES algoritam. Napad zahtijeva 2
47 poznatih
izvornih tekstova što ga čini nepraktičnim za upotrebu.
MITIM napad osmišljen je 1977 godine[7]. MITIM napad ne ovisi o unutrašnjoj strukturi kriptografskog sistema na koji se primjenjuje već je
bitno da se prilikom šifriranja na izvorni tekst primjenjuje kompozicija više funkcije šifriranja s različitim ključevima kako bi se dobio
šifrant. Za izvođenje ovog napada napadaču je potrebna mogućnost kriptiranja i dekriptiranja te posjedovanje izvornog teksta i njemu
korespondentnog šifranta. Izvorni tekst P šifrira se pomoću funkcije E i ključeva K
1,K
2kako bi se dobio šifrant C. Dobiveni šifrant dešifrira
se primjenom deskripcijske funkcije D i početnih ključeva K
1,K
2.
C=E(E(P,K1),K2)
P=D(D(C,K2),K1)
| (5.9) |
Napadač izračunava E(P,K
1) za sve moguće ključeve K
1 i D(C,K
2) za sve moguće ključeve K
2. Sve identične vrijednosti dobivene ovim postupkom
mogu otkriti točne ključeve šifriranja. Dobivene vrijednosti moguće je dodatno potvrditi provodeći postupak nad nekoliko parova izvornih
tekstova i šifranata. Ova vrsta napad jedan je od razloga zašto je DES algoritam bio zamijenjen s 3DES algoritmom.
Kriptoanaliza većine asimetričnih algoritama današnjice svodi se na rješavanje matematičkih problema faktorizacije velikih prirodnih
brojeva i/ili pronalaženje diskretnog logaritma [2][7]. Algoritme faktorizacije moguće je podijeliti na one bazirane na metodi specijalne
namjene i na opće metode. Metode specijalne namjene najčešće se koriste za faktoriziranje brojeva malih faktora dok opće metode imaju opću
primjenu te se često koriste u kriptoanalizi odnosno kriptografiji. Složenost metoda opće namjene ovisi o redu veličine broja koji se faktorizira.
Pollardova p-1 metoda razvijena je 1974 godine te spada u specijalne metode faktorizacije. Zasnovana je na Malom Fermatovom teoremu. Ukoliko
je
n broj koji treba faktorizirati i p neki njegov prosti faktor tada vrijedi:
|
am mod p=1 za svaki višekratnik od p-1
| (5.10) |
Pronalaskom
m uz pomoć (a
m-1,n) moguće je identificirati faktor od
n. Pronalazak višekratnika od
p-1 moguće je efikasno napraviti ukoliko
se on sastoji samo od malih prostih faktora. Pretpostavi se da su svi faktori broja
p-1 manji ili jednaki B te da su sve potencije prostih
brojeva koji dijele broj
p-1 manje od B. Tada je
m najmanji zajednički višekratnik brojeva od 1 do B. Ova metoda u najgorem slučaju nije ništa
lošija od običnog dijeljenja. Efikasnost ove metode izuzetno je ovisna o karakteristici broja
p-1[2].
Najefikasniji algoritam faktorizacije brojeva je NFS(Number field Sive) koji je moguće promatrati kao unaprijeđenu metodu kvadratnog sita,
koja je varijanta metode faktorske baze odnosno Fermatove faktorizacije[2]. Fermatova faktorizacija zasniva se na činjenici:
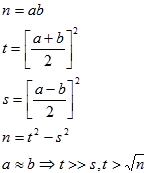
| (5.11) |
Algoritam počinje provjeru od broja
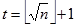
te traži
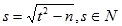
. Ukoliko ne uspije poveća t za jedan
i ponavlja se dok ne nađe takav broj. Jednom kad nađe brojeve t i s iz njih izračuna a i b te je broj n faktoriziran. Još neke opće metode
faktorizacije su: Eulerova metoda, Dixonova metoda i metoda isključivanja.
Problem pronalaženja diskretnog logaritma je za neki prosti broj p i elemente a i b naći x tako da vrijedi:
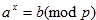
| (5.12) |
Jedan od efikasnih algoritama za rješavanje ovog problema je Indeks-calculus algoritam[7]. On služi za izračunavanje diskretnog logaritma
u poljima oblika F
p i
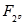
, gdje je p prost broj. Osnovna ideja ovog algoritma temelji se na :
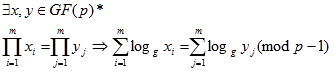
| (5.13) |
Uz dovoljan broj navedenih jednadžbi i relativno malen broj elemenata x
i i y
j sustav je rješiv.
Algoritam je moguće podijeliti u 5 koraka:
1. Isprazni se lista relacija
2. Za k={1,2…} uz pomoć cjelobrojne faktorizacije prilagođenje za glatke brojeve faktorizira se ak mod p po faktorskoj bazi.
Sprema se svaki pronađeni k i njemu odgovarajuću faktorizaciju kao relaciju. Ako je novo dodana relacija linearno nezavisna
od prethodno dodanih relacija zadržava se. Jednom kad se skupi r+1 takva relacija prestaje traženje novih relacija. r je veličina faktorske baze.
3. Formira se matrica čiji redovi predstavljaju relacije.
4. Matrica se svede na reducirani kanonski oblik odnosno prvi red je diskretni logaritam od -1 drugi od 2 itd.
5. Za s={0,1,2…} pokuša se faktorizirati as*b mod p po faktorskoj bazi. Kad se pronađe faktorizacija vraća se 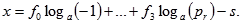
Moderni asimetrični kriptosustavi se od navedenih postupaka brane pažljivim odabirom operanada tako da je algoritme nemoguće izvesti u realnom vremenu.
Kako se hash algoritmi dosta koriste za ostavljanje digitalnog potpisa i autentifikacije napadi su često usmjereni na realizaciju mogućnosti
zloporabe digitalnog potpisa te mogućnost lažne autentifikacije. Dvije poznate vrste napada na hash funkcije su rođendanski napad i Rainbow table[7].
Rođendanski napad na hash funkciju traži kolizije u hash funkciji, a vrši se na sljedeći način:
1. Pripremaju se dvije inačice dokumenta. Jedna dobronamjerna i jedna zlonamjerna.
2. Za svaku od inačica pripremi se mnogo varijanti istog smisla. Primjer izrada više varijanti istog dokumenta prikazan je na slici 5-1.
|
Suprotno ljudskoj intuiciji sasvim/vrlo je lako/jednostavno napraviti/izraditi velik broj verzija/varijacija istog teksta bez promjene/
mijenjanja smisla/značenja.
Gornja rečenica ima 26 tj. 64 različite verzije.
|
Slika 5-1 Izrada više tekstova istog značenja
3. Potom je potrebno pronaći dvije inačice, jednu dobronamjernu i jednu zlonamjernu, koje imaju isti hash.
4. Zbog toga što inačice imaju isti hash imaju i isti potpis. Dovoljno je nekome dati dobronamjerni dokument da ga potpiše i kasnije je
moguće tvrditi da je potpisao zlonamjerni dokument.
Rođendanski napad moguće je spriječiti promjenom dokumenta prije njegova potpisivanja jer mu se na taj način mijenja vrijednost hash-a.
Druga vrsta napada na hash funkciju je Rainbow table [7]. Radi se o prethodno pripremljenoj tablici koja od hash-a generira izvorni
tekst. Prilikom autentifikacije passwordi se hashiraju te uspoređuju s prethodno spremljenim unosom odnosno njegovim hashem. Ukoliko su
hashevi isti pristup biva odobren. Ukoliko netko ukrade hash vrijednosti njihovim unošenjem prilikom autentifikacije neće ući u sustav
zato jer će sustav hashirati te vrijednosti i vratiti kako password ne odgovara korisniku. Kako bi uz pomoć hash vrijednosti kradljivac
ušao u sustav potrebno mu je iz nje razaznati izvorni tekst passworda ili naći password istog hasha. Tako što moguće je idućim algoritmom:
1. Definira se redukcijska funkcija R koja za dobiveni hash generira tekst P. R ne mora biti inverz hash funkcije.
2. Uzastopnom primjenom hash funkcije i redukcijske funkcije formiraju se hash lanci. Primjer hash lanca prikazan je na slici 5-2 preuzetoj
s adrese: http://en.wikipedia.org/wiki/Rainbow_table .
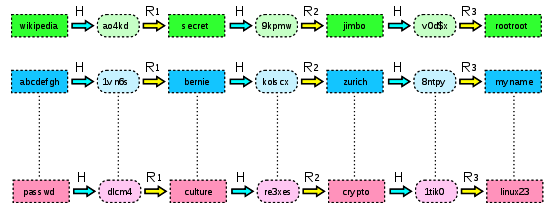 | |
Slika 5-2 Hash lanac
3. Početak i kraj svakog hash lanca sprema se u tablicu.
4. Uzima se hash vrijednost h za koju se želi dobiti izvorni tekst ili neki njemu iste hash vrijednosti. Na vrijednost h se uzastopno
primjenjuje redukcijska funkcija R i hash funkcija H dok se ne pojavi vrijednost jednaka jednoj od krajnjih vrijednosti u tablici.
5. Uzima se početna vrijednost koja odgovara dobivenoj krajnjoj vrijednosti te se razvija hash lanac. Postoji dobra šansa da lanca sadrži
vrijednost h. Ona vrijednost koja prethodi h je traženi password.
Rainbow table algoritam radi nešto drukčije od navedenog, ali zasniva se na istoj ideji. Kod njega se koristi niz više redukcijskih funkcija
te ukoliko dva lanca u istoj iteraciji postignu istu hash vrijednost jedan se izbacuje jer je duplikat.
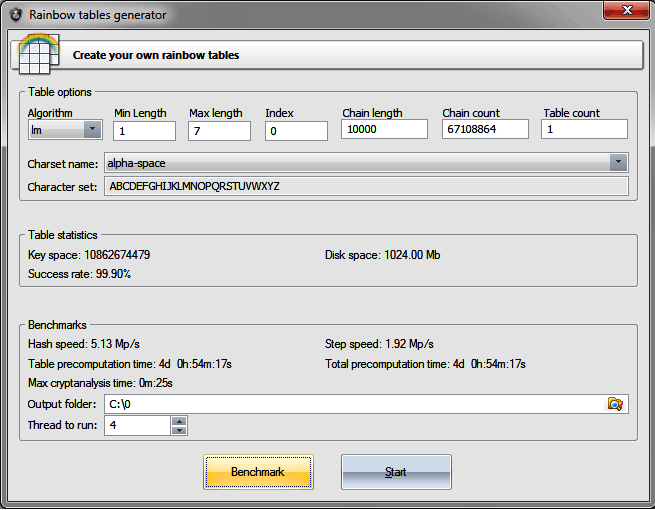 | |
Slika 5.3 Sučelje programa koji radi rainbow tablice
Slika 5-3 prikazuje sučelje programa koji generira rainbow tablice, a preuzeta je s:
http://www.passcape.com/windows_password_recovery
_rainbow_table_generator.Način obrane od Rainbow table algoritma je korištenjem relativno velikog nasumičnog dodatka prilikom svakog
hashiranja. Dodatak osigurava jedinstvenost svakog hashiranja.
|
DH(password)=H(H(password)+Dodatak)
| (5.14) |


 Pdf verzija
Pdf verzija
 Prezentacija
Prezentacija
 Ki
Ki001100]se razlikuju u barem dva bita v. Za svaku S-kutiju i svaki ulazni podatak Bij i sve e,f e {0, 1} vrijedi S[Bij]
S[Bij
00ef00].
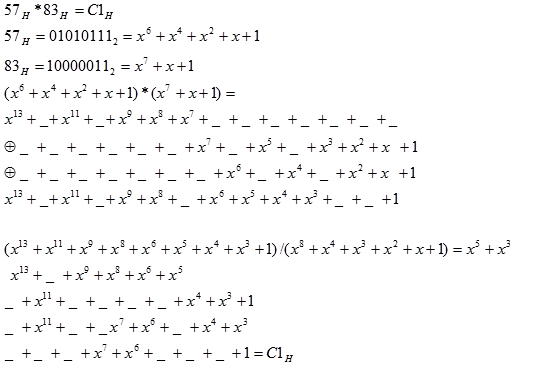
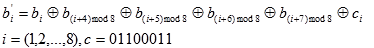

 (n). Ako je n prosti broj p tada je
(n). Ako je n prosti broj p tada je  (p)=p-1. Ako n nije prosti
broj,
(p)=p-1. Ako n nije prosti
broj, 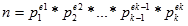 onda vrijedi:
onda vrijedi:
 (n)=n*
(n)=n*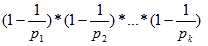
 (n)=n*
(n)=n*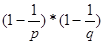 =(p-1)*(q-1)
=(p-1)*(q-1)  (n) mod n =1, za svaki a element od Zn*
(n) mod n =1, za svaki a element od Zn*
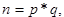 gdje su p i q prosti brojevi
gdje su p i q prosti brojevi 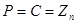 te vrijedi:
te vrijedi: 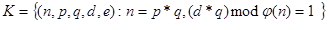
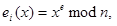
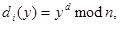 x,y e Zn
x,y e Zn
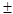 1 i q
1 i q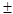 1 sadrže barem jedan veliki prosti faktor jer postoje efikasne metode
faktoriziranja brojeva koji sadrže samo male proste faktore. Nakon određivanja p i q izračunava n=p*q, a potom
1 sadrže barem jedan veliki prosti faktor jer postoje efikasne metode
faktoriziranja brojeva koji sadrže samo male proste faktore. Nakon određivanja p i q izračunava n=p*q, a potom  (n). Odabire se broj e<
(n). Odabire se broj e< (n),
takav da je relativno prost u odnosu na
(n),
takav da je relativno prost u odnosu na  (n). Uz pomoć e i
(n). Uz pomoć e i  (n) se izračunava d, tako da vrijedi:
(n) se izračunava d, tako da vrijedi:
 (n)= 1
(n)= 1




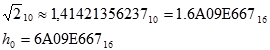
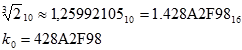

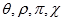 i
i 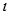 .
.
funkcija, prikazana slikom 4-3 preuzetoj iz [5] izračunava paritet svakog stupa matrice te nad svakim elementom matrice provodi XOR s XOR-om pariteta dvaju predodređenih stupaca. Matematički je funkciju moguće zapisati kao:
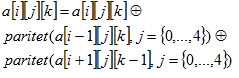

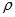 funkcija rotira svaku od 64-bitnih riječi za različiti trokutasti broj mjesta. Rad funkcije prikazan je na slici 4-4 preuzetoj
iz [5] . Trokutasti brojevi su brojevi oblika Br=
funkcija rotira svaku od 64-bitnih riječi za različiti trokutasti broj mjesta. Rad funkcije prikazan je na slici 4-4 preuzetoj
iz [5] . Trokutasti brojevi su brojevi oblika Br=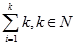 Matematički je postupak funkcije moguće zapisati kao:
Matematički je postupak funkcije moguće zapisati kao:
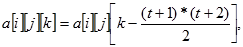 za t=0,…,24 i
za t=0,…,24 i 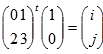

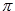 je transpozicija stanja.
je transpozicija stanja. 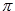 funkcija prikazana je na slici 4-5 preuzetoj iz [5] Matematički ju je moguće zapisati kao:
funkcija prikazana je na slici 4-5 preuzetoj iz [5] Matematički ju je moguće zapisati kao:
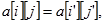
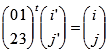

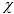 je jedina nelinearna operacija u SHA-3. Svaki element matrice XOR-a se s XOR-om pariteta dvaju predodređenih redova kao što je
prikazano na slici 4-6 preuzetoj iz [5] . Matematički je operaciju moguće prikazati kao:
je jedina nelinearna operacija u SHA-3. Svaki element matrice XOR-a se s XOR-om pariteta dvaju predodređenih redova kao što je
prikazano na slici 4-6 preuzetoj iz [5] . Matematički je operaciju moguće prikazati kao:
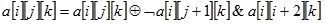

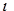 operacija svaki element XOR-a s konstantnom vrijednošću RC[zr]. Matematički se prikazuje kao:
operacija svaki element XOR-a s konstantnom vrijednošću RC[zr]. Matematički se prikazuje kao:
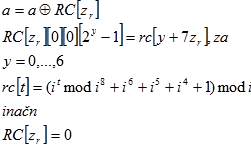

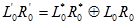 naziva se input tj. ulazni XOR, a šifranata output tj. izlazni XOR, a zajedno čine diferencijal.
Na primjeru DES algoritma moguće je sagledati ideju postupka diferencijalne kriptoanalize te ju razložiti u tri koraka:
naziva se input tj. ulazni XOR, a šifranata output tj. izlazni XOR, a zajedno čine diferencijal.
Na primjeru DES algoritma moguće je sagledati ideju postupka diferencijalne kriptoanalize te ju razložiti u tri koraka:
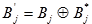 i Cj definira se :
i Cj definira se :
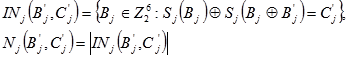
 Ki za ulazni podatak S-kutije u i-toj rundi. Zbog provedenih operacija vrijedi:
Ki za ulazni podatak S-kutije u i-toj rundi. Zbog provedenih operacija vrijedi:
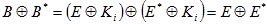
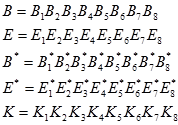
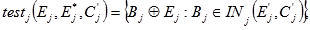
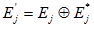
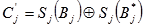
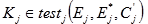
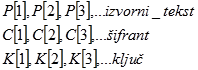
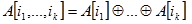
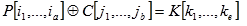
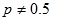 . Vjerojatnost desne strane dobiva se njenim izračunavanjem za veliki
broj parova izvorni tekst, šifrant.
III. Ako je u više od pola slučajeva na lijevoj strani nula i
. Vjerojatnost desne strane dobiva se njenim izračunavanjem za veliki
broj parova izvorni tekst, šifrant.
III. Ako je u više od pola slučajeva na lijevoj strani nula i 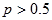 za vrijednost se uzima nula, a za
za vrijednost se uzima nula, a za 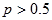 se uzima jedan. Na taj način dobiva
se linearna jednadžba u bitovima ključa. Uz dovoljno velik broj takvih jednadžbi postaje moguće odrediti ključ.
IV. Kako bi metoda bila uspješna kod DES algoritma preporuča se uzimanje
se uzima jedan. Na taj način dobiva
se linearna jednadžba u bitovima ključa. Uz dovoljno velik broj takvih jednadžbi postaje moguće odrediti ključ.
IV. Kako bi metoda bila uspješna kod DES algoritma preporuča se uzimanje 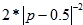 parova izvornog teksta i šifranta.
Linearnu kriptoanalizu prvi je opisao Mitsuru Matsui 1993. godine kao teoretski napad na DES algoritam. Napad zahtijeva 247 poznatih
izvornih tekstova što ga čini nepraktičnim za upotrebu.
parova izvornog teksta i šifranta.
Linearnu kriptoanalizu prvi je opisao Mitsuru Matsui 1993. godine kao teoretski napad na DES algoritam. Napad zahtijeva 247 poznatih
izvornih tekstova što ga čini nepraktičnim za upotrebu.
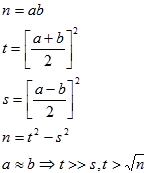
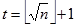 te traži
te traži 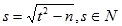 . Ukoliko ne uspije poveća t za jedan
i ponavlja se dok ne nađe takav broj. Jednom kad nađe brojeve t i s iz njih izračuna a i b te je broj n faktoriziran. Još neke opće metode
faktorizacije su: Eulerova metoda, Dixonova metoda i metoda isključivanja.
. Ukoliko ne uspije poveća t za jedan
i ponavlja se dok ne nađe takav broj. Jednom kad nađe brojeve t i s iz njih izračuna a i b te je broj n faktoriziran. Još neke opće metode
faktorizacije su: Eulerova metoda, Dixonova metoda i metoda isključivanja.
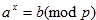
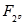 , gdje je p prost broj. Osnovna ideja ovog algoritma temelji se na :
, gdje je p prost broj. Osnovna ideja ovog algoritma temelji se na :