ECDSA - Eliptic Curve Digital Signature Algorithm
 

Naslovnica

Uvod

ECDSA

Download

Linkovi

ECDSA (engl. elliptic curve digital signature algorithm) je algoritam za digitalni potpis poruke koji koristi eliptične krivulje i njihova svojstva.

Parametri kriptosustava:

Uređena šestorka D = (q, a, b, P, n, h) predstavlja parametre kriptosustava za koje vrijedi
q = p ili q = 2^m , p je prosti broj
         - a, b su elementi polja , određuju jednadžbu eliptične krivulje
         - P je točka na krivulji E, P = (x_p, y_p)
         - n je red točke P , najmanji pozitivni cijeli broj takav da vrijedi nP = O
         - h = #E(F_q)/n.

          Prethodno navedeni parametri su javni.

Izbor parametara:

         Dva su osnovna koraka kod izbora parametara za kriptosustav zasnovan na eliptičkim krivuljama:

• izbor konačnog polja ,

• izbor eliptičke krivulje E nad .

         Kod izbora polja, dvije su osnovne mogućnosti: ili je q = p prost broj ili q = 2^m potencija broja 2. Ako su p i 2^m približno iste veličine, ova dva izbora pružaju istu razinu sigurnosti.

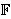         Među poljima , da mi se minimiziralo vrijeme potrebno za modularno množenje, preporuča se da p ima oblik 2^k 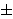c za neki mali prirodni broj c (npr. Mersenneovi prosti brojevi oblika 2^k - 1, 2¹⁶⁰ + 7, 2²⁵⁵ + 95, i sl.).

         Kod polja karakteristike 2, osim broja elemenata, moramo odabrati i način reprezentacije elemenata. Najčešće se koriste trinomijalne i optimalne normalne baze. Kao što smo ranije napomenuli, izbor takvih baza omogućuje efikasniju implementaciju. No, takve baze ne postoje za svako konačno polje karakteristike 2, pa i to utječe na izbor polja. Neki popularni izbori su npr. 2¹⁶³, 2¹⁹¹, 2²³⁹ i 2⁴³¹.

         Kod izbora eliptičke krivulje trebamo paziti da problem diskretnog logaritma bude "težak". Kako smo već više puta napomenuli, ECDLP je, prema svemu što vam je danas poznato, vrlo težak problem. Međutim, postoje tipovi eliptičkih krivulja kod kojih je taj problem nešto (ali čak puno) lakši. Zato takve krivulje treba izbjegavati. Situacija je vrlo slična kao kod kriptosustava koji svoju sigurnost zasnivaju na teškoći faktorizacije velikih prirodnih brojeva (npr. RSA ili Rabinov). I tamo je tvrdnja da je broj oblika pq, gdje su p i q veliki prosti brojevi, teško rastaviti na faktore točna samo ako se p i q odaberu pažljivo (npr. p i q ne smiju biti jako bliski; brojevi p - 1 i q - 1 moraju imati barem jedan veliki prosti faktor).

         Algoritam:

1. ECDSA generiranje ključeva.
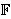E je eliptička krivulja nad , a P je točka prostog reda n na E(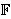). Svaki korisnik napravi sljedeće:

a) Izabere slučajan broj d iz skupa {1, ... , n - 1};
b) Izračuna Q = [d] P;
c) Q je javni, a d tajni ključ.

2. ECDSA generiranje potpisa.
Kad želi potpisati poruku m, Alice radi sljedeće:

a) Izabere slučajan broj k iz skupa {1, ... , n - 1};
b) Izračuna [k] P = (x₁, y₁) i r = x₁ mod n. Ako je r = 0, onda se vrati na korak a);
c) Izračuna k^-1 mod n;
d) Izračuna s = k^-1(H(m) + dr) mod n, gdje je H hash funkcija. Ako je s = 0, onda se vrati na korak a);
e) Potpis poruke m je uređeni par prirodnih brojeva (r, s).

3. ECDSA provjera potpisa.
Da bi verificirao Alicein potpis (r, s) poruke m, Bob treba napraviti sljedeće:

a) Dobiti Alicein javni ključ Q;
b) Provjeriti da su r i s cijeli brojevi iz skupa {1, ... , n - 1};
c) Izračunati w = s^-1 mod n i H(m);
d) Izračunati u₁ = H(m)w mod n i u₂ = rw mod n;
e) Izračunati [u₁] P + [u₂] Q = (x₀, y₀) i v = x₀ mod n;
f) Prihvatiti potpis kao vjerodostojan ako i samo ako je v = r.

 

Programsko ostvarenje:

Algoritam je ostvaren u programskom jeziku C korištenjem biblioteka GMP i ECC-LIB-2.0.

Korištene funkcije iz biblioteke ECC-LIB-2.0:

void CMmethod(int D, mpz_t * p1, mpz_t * m1, mpz_t * curv)
         -vraca red p1 konacnog polja, elipticku krivulju curv i njezin red m1 na temelju diskriminante D

void domain_parameters(mpz_t * curv, mpz_t * base_point, mpz_t * p, mpz_t * m, mpz_t * n, mpz_t * h)
          -kreira tocku generator reda n i vraca brojeve n i h, gdje je n*h=m(red krivulje)

void create_priv_and_public(mpz_t * curv, mpz_t * p, mpz_t * base, mpz_t * my_private, mpz_t * my_public)
          -kreira privatni i javni kljuc koristeci tocku generator

void print_curve(mpz_t * curv)
          -ispisuje krivulju

void print_point(mpz_t * point)
          -ispisuje tocku

void add_point(mpz_t * curv, mpz_t * p1, mpz_t * p2, mpz_t * p3, mpz_t * p)
          -zbraja 2 tocke modulo p

void point_mult(mpz_t * curv, mpz_t * p1, mpz_t * k, mpz_t * result, mpz_t * p)
          -mnozi tocku sa skalarom modulo p

void rand_point(mpz_t * curv, mpz_t * p, mpz_t * base)
          -generira slucajnu tocku na eliptickoj krivulji

 

Izvorni kod programa, izvršna datoteka i biblioteka ECC-LIB-2.0 su dostupni za download unutar .tar paketa: ecdsa.tar

Biblioteka GMP je dostupna na slijedećem linku: http://www.swox.com/gmp

sigurnost.zemris.fer.hr