Ažuriraj vrijednosti sjemenki:
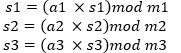
Izračunaj nasumični broj u u intervalu (0, 1):
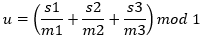
Linearni kongruencijalni generator (LCG) je algoritam koji daje niz pseudoslučajnih brojeva izračunatih s diskontinuiranom djelomičnom linearnom jednadžbom(engl. discontinuous piecewise linear equation). Djelomično linearna funkcija je funkcija definirana na (moguće neograničenom) intervalu realnih brojeva, tako da postoji zbirka intervala na svakom od kojih je funkcija afina funkcija. Afina funkcija je funkcija koja preslikava afini prostor na sebe, a pritom zadržava i dimenziju svih afinih podprostora (što znači da šalje točke u točke, pravce u pravce, ravnine u ravnine i tako dalje) i omjere duljina paralelnih segmenti linije. Linearni kongurencijalni generator jednostavan je za izvesti i lako se izvršava na strojevima koji imaju mogućnost “modulo” operacije, sama jednadžba LCG-a glasi:
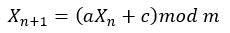
Gdje je X sekvenca pseudoslučajnih brojeva, te:
Ovisno o vrijednostima parametra c linearni kongruencijalni generator se naziva:
Uz dani početni broj (engl. seed), linearni kongruencijalni generator će uvijek proizvoditi isti niz brojeva.
Linearni kongruencijalni generatori imaju period, što znači da će se slijed na kraju ponoviti. Duljina perioda ovisi o parametrima (a, c i m). Dok su linearni kongruencijalni generatori sposobni proizvesti pseudoslučajne brojeve koji mogu proći formalne testove slučajnosti, kvaliteta izlaza je izuzetno osjetljiva na izbor parametara m i a. Zbog svoje determinističke prirode, linearni kongruencijalni generatori nisu prikladni za kriptografske svrhe gdje je potrebna velika razina slučajnosti.
Hash_DRBG je kriptografski siguran generator pseudoslučajnih brojeva standardiziran od strane NIST-a u SP 800-90A. Koristi hash funkciju (poput SHA-256 ili SHA-512) za generiranje pseudoslučajnih bitova. Ista hash funkcija se treba koristiti u cijelom procesu generiranja pseudoslučajnog broja. Vrijednosti V i C su kritične vrijednosti unutarnjeg stanja, o kojima ovisi sigurnost za ovaj DRBG mehanizam.
Proces generiranja pseudoslučajnog broja započinje inicijalizacijom početnog stanja preko „Hash_DRBG Instantiate Process“:
Gdje „||“ označava konkatenaciju, a „Hash_df“ derivacijsku funkciju koja hashira dani niz znakova i vraća traženi broj bitova. Završetkom tog procesa se dobiva početno stanje (vrijednosti V, C i reseed_count) Dobivene vrijednosti daju se „Hashgen“ funkciji koja stvara novi hash, ako je odabrano da se želi generirati više brojeva, onda se treba ići u reseed process kojim se određuju nove vrijednosti V, C i reseed_count. U nastavku se nalazi jednostavni prikaz rada generatora, gdje je većina internih procesa izostavljena.
Mersenne Twister je algoritam za generiranje pseudoslučajnih brojeva. Razvili su ga Makoto Matsumoto i Takuji Nishimura 1997. godine. Jedan je od najčešće korištenih generatora nasumičnih brojeva zbog svoje velike brzine, kvalitete generiranih brojeva i dugog perioda. Ime mu potječe od korištenja Mersenneovog prostog broja za određivanje duljine perioda. Mersenneov prosti broj je oblika 2^n-1 za neki cijeli broj n. Najčešće korištena verzija Mersenne twister algoritma je MT19937 koji se temelji na Mersenneovom prostom broju 2^19937-1 i koristi 32-bitnu duljinu riječi.
Za generiranje pseudoslučajnih w-bitnih cijelih brojeva u rasponu [0,2w-1], Mersenne Twister koristi linearnu rekurziju nad binarnim poljem F2. Algoritam se temelji na twisted generalised feedback shift registru (twisted GFSR ili TGFSR) u "racionalnom normalnom obliku"(TGFSR(R)). Temeljna ideja je definirati niz x_i putem jednostavne rekurzije i potom izračunati brojeve oblika xiT, gdje je T inverzna F2 matrica zvana tempering matrica.
S odabirom vrijednosti gdje je 2(nw-r) - 1 Mersenneov prost broj
Stanje potrebno za implementaciju Mersenne twistera je niz od n w-bitnih vrijednosti. Niz x inicijalizira se sljedećim izrazom:
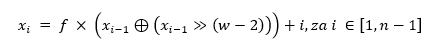
Niz x je definiran rekurzijom:
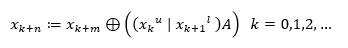
gdje:
Twist transformacija A je definirana u racionalnom normalnom obliku kao:
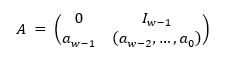
gdje je I_(w-1) jedinična matrica dimenzija (w-1)×(w-1). Pomnožimo li x matricom A, račun se svodi na:
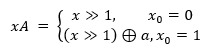
Na novo generirani broj još se primjenjuje i tempering transformacija koja se sastoji od sljedećih bitovnih operacija:
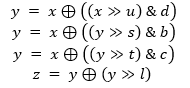
gdje x označava sljedeću vrijednost iz niza, y privremenu vrijednost, a z konačni izlaz algoritma.

Generator slučajnih brojeva Wichmann-Hill je algoritam za generiranje pseudoslučajnih brojeva kojeg su predstavili Brian Wichmann i David Hill 1982. godine. Ovaj generator kombinira tri linearna kongruencijalna generatora kako bi postigao dulji period i poboljšao statističke osobine u usporedbi s pojedinačnim generatorima.
Algoritam koristi tri zasebna linearna kongruencijalna generatora s različitim modulima i multiplikatorima. Svaki generator proizvodi niz cijelih brojeva, koji se zatim kombiniraju kako bi se dobio konačni nasumični broj u intervalu (0,1). Parametri:
Koraci algoritma:
Ažuriraj vrijednosti sjemenki:
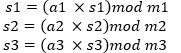
Izračunaj nasumični broj u u intervalu (0, 1):
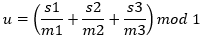
Pseudokod za generator glasi:
Inicijaliziraj s1, s2, s3 s početnim vrijednostima
Za svako generiranje nasumičnog broja:
s1 = (171 * s1) mod 30269
s2 = (172 * s2) mod 30307
s3 = (170 * s3) mod 30323
u = (s1 / 30269.0 + s2 / 30307.0 + s3 / 30323.0) mod 1.0
Vrati u
Lagged Fibonacci generator (LFG) je metoda generiranja pseudoslučajnih brojeva koja se temelji na modifikaciji poznatog Fibonacci niza. Fibonaccijev niz dan je izrazom:
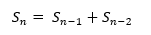
Problem s korištenjem običnog Fibonaccijevog niza je što bi pseudoslučajni nizovi bili jako predvidivi. Zato se umjesto tog izraza, koristi sljedeći:
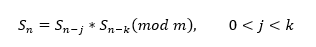
Umjesto da sljedeći u nizu računamo tako da zbrajamo posljednja dva, biramo brojeve j i k koji označavaju koje ćemo brojeve koristiti. Također, nije nužno koristiti operaciju množenja. Umjesto zvjezdice u izrazu možemo iskoristiti zbrajanje, oduzimanje, množenje ili XOR. Na početku izvođenja, uz gore navedene parametre, generatoru se mora dati i seed. Seed su brojevi koji će se koristiti kao početni niz.
Prednosti generatora LFG su:
Nedostatci:
Inversive congruential generator
Generiranje pseudo-slučajnih brojeva u ICG-u definira se formulom:
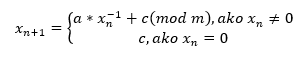
Gdje su:
Nakon određenog broja koraka, algoritam će krenuti ponavljati brojeve. Najveći period ponavljanja je broj m. Kako bi algoritam generirao što više različitih brojeva prije nego što počne ispočetka, potrebo je odabrati što bolje parametre. Postoji nekoliko algoritama za odabir parametara, ali jedan od njih je odabrati brojeve takve da prsten polinoma
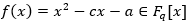
bude primitivan.
Xorshift je jednostavan algoritam za generiranje pseudoslučajnih brojeva. Izumio ga je George Marsaglia 2003 godine. Jedan je od najbržih softverskih generatora pa se vrlo često koristi. Generiraju niz brojeva od početnih uvjeta koristeći logički pomak i operaciju isključivo ili. Sam generator ne može proći statističke testove pa se trebaju kombinirati s nekim ne linearnim funkcijama. Postoji perioda ponavljanja koja je povezana s duljinom riječi pa za generator s velikom periodom treba odvojiti dovoljno memorije. Postoji 32, 64, 128 i 1024 bitni xorshift. Što je veći broj bita to je algoritam više slučajan. Verzije veće od 64 bita su sporije na današnjem hardveru. Xorshift se danas koristi u simulacijama, igrama i ugrađenim sustavima gdje su resursi ograničeni i vrijeme bitno.
Algoritam je vrlo jednostavan i učinkovit. Odabire se početno stanje i rade se operacije
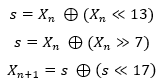
Gdje je a ≪ b operacija logičkog pomaka broja a u lijevo za b mjesta, a ≫ b je ekvivalentna operacija za desno micanje, a a ⊕ b je operacija logičkog isključivog ili.
Pravilo 30 generatori su generatori koji koriste jednodimenzionalni stanični automat. Stanični automat je sličan Conwayevoj Igri života, ali u jednoj dimenziji, tj. pravilo stanja za svaku ćeliju je funkcija trenutnog stanja i stanja susjeda. Ćelije mogu biti predstavljene kao niz bitova. Generator je osmislio Stephen Wolfram, a koristi se u aplikaciji Wolfram Alpha, poznatoj aplikaciji za rješavanje matematičkih problema. Algoritam se često koristi jer je brz i relativno jednostavan za izradu. Također je zanimljiv zbog svoje povijesti i jer koristi zanimljive koncepte. Svoj naziv je dobio jer binarni broj 00011110 u dekadskom zapisu glasi 30. Pravilo se također može zapisati kao novo stanje = lijevi susjed XOR (staro stanje OR desni susjed).
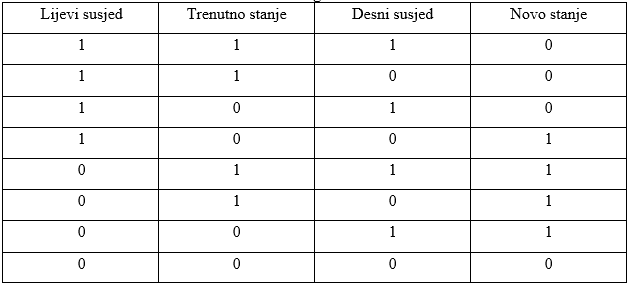
Na početku automat treba inicijalizirati slučajnim seedom. Tada ga se pusti da se brojevi mijenjaju po zadanim pravilima (Tablica 2.2). Nakon svakog primjenjivanja pravila, uzme se broj u sredini kao slučajni bit. Ako je broj bitova paran, nije bitno uzima li se lijevi ili desni bit od sredine. Lista brojeva se vrti u krug (poslije zadnjeg elementa ide prvi) pa se tako rješava problem desnog susjeda zadnjeg elementa i lijevog susjeda prvog elementa.