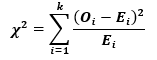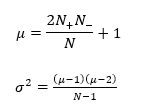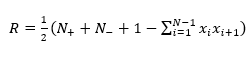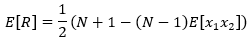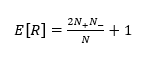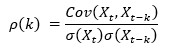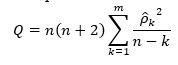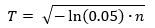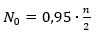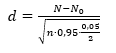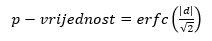Testovi

Wald-Wolfowitz runs test

Uvod i definicija

Wald–Wolfowitzov test (engl. Wald–Wolfowitz runs test) je statistički test bez parametara koji provjera hipotezu o slučajnosti nad nizom podataka s dvije vrijednosti, odnosno, jesu li elementi niza međusobno neovisni. Nazvan je po statističarima Abrahamu Waldu i Jacobu Wolfowitzu. Test odgovara na pitanje “Jesu li ovi uzorci podataka generirani nasumičnim procesom?”. Prvi korak u runs testu je brojanje broja izvoda u nizu podataka. Postoji nekoliko načina za definiranje izvoda ovisno o setu podataka nad kojim se provodi test. Najlakši primjer za to prikazati je bacanje novčića; gdje će sekvenca podataka izgledati npr. G G P G P G P P G G za 10 bacanja novčića (G - glava, P - pismo). Što se može isto prikazati kao niz ++-+-+--++, koji se sastoji od 7 izvoda duljina 2, 1, 1, 1, 1, 2, 2. Test se temelji na nultoj hipotezi, odnosno, da je svaki element u nizu neovisno izvučen iz iste distribucije.

Pod nultom hipotezom, broj izvoda u nizu od N (N=N₊+N_-) elemenata je slučajna varijabla čija uvjetna distribucija, s obzirom na promatranje N₊ pozitivnih vrijednosti i N_-- negativnih vrijednosti, približno normalna s prosjekom i varijancom:

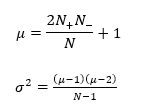
te brojev izvoda

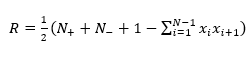
Očekivani broj izvoda, pretpostavljajući neovisnost događaja, računa se:

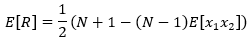
što kada se x_1 x_2 raspišu, te pojednostavni se u:

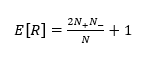
Rezultat testa dobiva se uspoređivanjem dobivenog broja izvoda s očekivanim brojem izvoda. Ukoliko je dobiveni broj izvoda mnogo veći ili manji od očekivanog broja izvoda, hipoteza o nezavisnosti slučajnih događaja može biti odbačena. Statistička značajnost kako bi se odredilo što je “mnogo veće” ili “mnogo manje”, izabire se prije prikupljanja podataka, i tipično iznosi oko 5%, što za Wald–Wolfowitzov test tipično nije slučaj, više o tome u primjerima.

Test se koristi za testiranje:

• Slučajnost distribucije - uzimanjem podataka po redu i označavanjem s “+” sve podatke veće od prosjeka, te s “-” sve podatke manje od prosjeka, ignorirajući podatke jednake prosjeku.
• Odgovara li funkcija dobro skupu podataka- podaci koji prelaze vrijednost funkcije, označuju se s “+”, dok ostali s “-”. U obzir se uzima samo je li podatak iznad ili ispod predviđene vrijednosti funkcije, ali ne i koliko je “udaljeno”.

Autocorrelation test

Uvod i definicija

Autokorelacija je statistički koncept koji procjenjuje stupanj korelacije između vrijednosti varijable u različitim vremenskim točkama i temeljni je koncept u analizi vremenskih serija. Autokorelacija mjeri stupanj sličnosti između dane vremenske serije i njezine pomaknute verzije tijekom uzastopnih vremenskih perioda. Slično je računanju korelacije između dvije različite varijable, osim što u autokorelaciji računamo korelaciju između dvije različite verzije X_t i X_{t - k} iste vremenske serije. Autokorelacija označava se s ρ(k) gdje k označava vremenski pomak ili broj intervala između opažanja. Izračunava se pomoću koeficijenta korelacije: Za skup podataka vremenske serije, autokorelacija na pomaku k određuje se usporedbom vrijednosti varijable u trenutku t s vrijednostima u trenutku t - k.

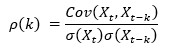
• Cov je kovarijanca
• σ je standardna devijacija
• X_t je vrijednost varijable u trenutku t

Pozitivna autokorelacija (ρ>0) ukazuje na tendenciju da vrijednosti u jednoj vremenskoj točki budu pozitivno povezane s vrijednostima u kasnijoj vremenskoj točki. Visoka autokorelacija na određenom pomaku sugerira snažnu linearnu vezu između trenutnih vrijednosti varijable i njezinih prošlih vrijednosti na tom pomaku. Negativna autokorelacija (ρ<0) sugerira obrnuti odnos između vrijednosti u različitim vremenskim intervalima. Niska ili nulta autokorelacija ukazuje na odsutnost linearne ovisnosti između trenutnih i prošlih vrijednosti varijable na tom pomaku.

Ljung-Box test

Ljung-Box test je statistički test koji se koristi za provjeru postojanja ukupne autokorelacije u vremenskoj seriji do određenog broja pomaka kk. Za razliku od testova koji ispituju autokorelaciju na pojedinačnim pomacima, Ljung-Box test istodobno provjerava postojanje autokorelacije na više pomaka, pružajući sveobuhvatan uvid u slučajnost serije.

Hipoteze testa:

• Nulta hipoteza (H_0): Nema autokorelacije u vremenskoj seriji do određenog reda k; podaci su nezavisni
• Alternativna hipoteza (H_1): Postoji autokorelacija u vremenskoj seriji za barem jedan pomak do reda k

Ljung-Boxova statistika Q izračunava se prema formuli:

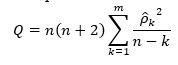
gdje je:

• n — ukupan broj opažanja u vremenskoj seriji
• m — maksimalni broj pomaka (lag) koji se testira
• ρ ̂__k — procijenjena autokorelacija na pomaku k.

Statistika Q prati χ² (chi-kvadrat) raspodjelu s m stupnjeva slobode.

Interpretacija rezultata:

• Visoka p-vrijednost (≥0.05): ne odbacuje se nulta hipoteza, nema statistički značajne autokorelacije u seriji do pomaka k, podaci mogu smatrati slučajnim u kontekstu testiranih pomaka
• Niska p-vrijednost (<0.05): odbacuje se nulta hipoteza, postoji značajna autokorelacija, podaci pokazuju obrazac koji nije slučajan

Chi-square test

1. Generiranje pseudo-nasumičnih brojeva
   Prvo je potrebno generirati što veći niz pseudo-nasumičnih brojeva.
2. Definiranje intervala
   Da bi se testirala ravnomjernost distribucije, opseg vrijednosti se dijeli na više intervala ili “binova”. Npr ako generiramo brojeve od 1 do 1000, možemo taj opseg podijeliti na 10 intervala, npr. 1-100, 101-200 itd. Pošto želimo da generator bude što nasumičniji, u svakom intervalu očekujemo otprilike jednak broj generiranih brojeva.
3. Brojanje stvarnih frekvencija
   Brojimo koliko se puta pojavio broj u svakom od intervala.

4. Primjenjivanje chi-square izraza

   

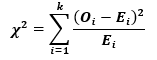
   O_i predstavlja stvarnu frekvencija u intervalu i E_i predstavlja očekivanu frekvencija u intervalu i. U prijašnjem primjeru svaki E_i za svaki interval će biti 100. k predstavlja broj intervala

5. Uspoređivanje s kritičnom vrijednošću Izračunatu vrijednost uspoređujemo s kritičnom vrijednosti iz chi-square tablice za zadanu razinu značajnosti (npr. 5% ili 1%) i stupnjeve slobode k - 1. Ako je izračunata vrijednost manja od kritične vrijednosti, ne možemo odbaciti hipotezu da su brojevi ravnomjerno raspodijeljeni, što ukazuje na to da generator vjerojatno dobro generira pseudo-nasumične brojeve. Ako je izračunata vrijednost veća od kritične vrijednosti, odbacujemo hipotezu, što ukazuje na odstupanja od ravnomjerne distribucije.

Test diskretnom fourierovom transformacijom

Uvod i definicija

Test diskretnom fourierovom transformacijom (DFT) je test koji napravi fourierovu transformaciju niza brojeva i tako ih prebaci iz vremenske u frekvencijsku domenu. Cilj toga je pronaći periodičnost niza. Da bi se pronašla periodičnost uzima se broj vrhove frekvencijske domene koja prelaze 95% svih frekvencija. Ako je broj prevelik generator nije uspio proći test.

Koraci izvođenja

• Stvori se određen broj slučajnih brojeva te se oni pretvore u binarni niz i spoje se zajedno
• Sve nule pretvorimo u -1
• Napravimo DFT na nizu
• Uzmemo magnitude M = |S'| gdje je S' prva polovica niza poslije DFT

• Izračunamo

  

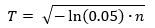
  što je 95%-tni vrh pod pretpostavkom da je niz nasumičan

• Izračunamo

  

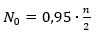
  što je broj vrhova nižih od T ako je razdioba zaista nasumična

• Nađemo K što je zapravo broj vrhova nižih od T

• Izračunamo

  

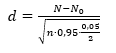
• Izračunamo

  

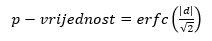
  gdje je erfc funkcija pogreške

Zaključak

Moramo odrediti koja nam granična p vrijednost. Standard je 1%, što znači ako je p vrijednost < 0.01 generator nije slučajan. Preporuča se što veći broj bitova za testiranje, minimum je 1000.