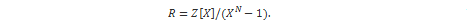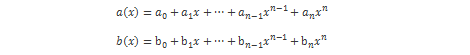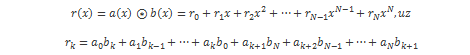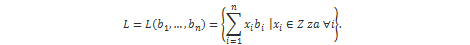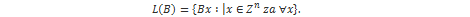Matematički preduvjeti
Kvocijentni prsten polinoma
NTRU kriptosustav koristi kvocijentni prsten polinoma:
Elementi tog prstena su polinomi stupnja manjeg od N s cjelobrojnim koeficijentima. Polinomi u prstenu se zbrajaju tako da se zbroje koeficijenti na istim pozicijama. Množenje polinoma unutar prstena R naziva se konvolucijsko množenje, oznake  . Konvolucijski umnožak polinoma a(x) i b(x):
. Konvolucijski umnožak polinoma a(x) i b(x):
definira se kao:
Konvolucijsko množenje je zapravo obično množenje polinoma uz redukciju potencija od x modulo N.
Još jedna važna operacija korištena u NTRU kriptosustavu je multiplikativni inverz polinoma. Inverz polinoma a modulo q je polinoma A za koji vrijedi:
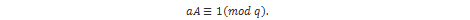 (4) Jednako vrijedi i za konvolucijsko množenje. [8][9][10]
(4) Jednako vrijedi i za konvolucijsko množenje. [8][9][10]
Rešetke
Neka je Rm m-dimenzijski euklidski prostor. Rešetka u Rm je skup svih mogućih kombinacija n linearno nezavisnih vektora iz Rm:
Vrijednosti n i m nazivaju se rang i dimenzija rešetke respektivno. Kaže se da je rešetka potpuno dimenzijska ako je n=m. U NTRU kriptosustavu upotrebljavati će se upravo takve rešetke. Slijed vektora  naziva se bazom rešetke i obično je predstavljen kao matrica gdje su vektori baze stupci. Upotrebljavajući matričnu notaciju, rešetka se može zapisati kao:
naziva se bazom rešetke i obično je predstavljen kao matrica gdje su vektori baze stupci. Upotrebljavajući matričnu notaciju, rešetka se može zapisati kao:
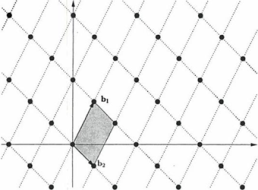
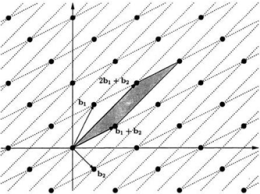
Duljina baze jednaka je duljini najduljeg vektora baze. Na slici 1 (lijevo) prikazana je dvodimenzionalna rešetka s vektorima baze b1=[1 2], b2=[1 -1]. Ista rešetka može imati više različitih baza. Na primjer baza rešetke na slici 1 (lijevo) može biti b1'=b1+b2=[2 1], b2'=2b1+b2=[3 3]. Mreže koje tvore vektori (b1, b2) i (b1', b2') su različite, ali presjecišta su na istim koordinatama kao što se vidi na slici 1. [11]
 |
 |
Teško rješivi problemi rešetke
Postoji nekoliko problema rešetki za koje se vjeruje da su NP teški:
- Problem najkraćeg vektora (engl. Shortest Vector Problem - SVP)
- Problem najbližeg vektora (engl. closest Vector Problem - CVP)
Algoritmi za njihovo rješavanje nazivaju se algoritmi redukcije rešetke. Formalna definicija redukcije rešetke bila bi nalaženje najkraće baze rešetke. Najbolji algoritmi za rješavanje ovog problema su ili eksponencijalne složenosti ili daju loše aproksimacijske rezultate. [11]
Problem najkraćeg vektora
Problem najkraćeg vektora definira se na sljedeći način: Za zadanu bazu rešetke, nađi najkraći ne-nul vektor rešetke.
Ne postoji algoritam polinomne složenosti za njegovo rješavanje. Postoji aproksimacijski algoritam (LLL algoritam [17]), koji u polinomnom vremenu nalazi vektor rešetke čija je duljina najviše y puta veća od duljine najkraćeg vektora rešetke. Faktor y se naziva aproksimacijski faktor. Najbolji aproksimacijski faktor jednak je (1.33)n/2, gdje je n dimenzija rešetke. Za bolje aproksimacije upotrebljava se BKZ [18] (Block Korkin-Zoloratev) algoritam od Schnorra i Euchnera.
Problem najbližeg vektora
Problem najbližeg vektora definira se kao: Za zadanu bazu rešetke B i vektor t nađi vektor rešetke v najbliži vektoru t.
Za CVP problem postoji aproksimacijski algoritam polinomne složenosti (Babai-jeva tehnika [19]). Aproksimacijski faktor jednak je 2*(1.33)n/2, gdje je n dimenzija rešetke.
|
|
|
|