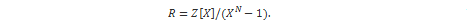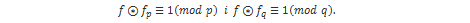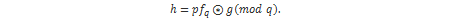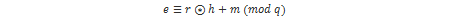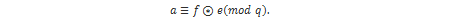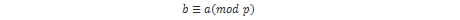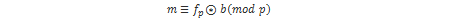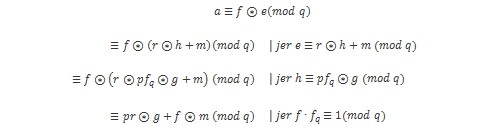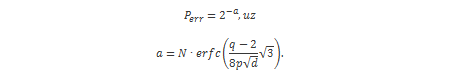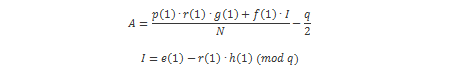NTRU kriptosustav

NTRU kriptosustav (engl. N-th degree TRUncated polynomial ring) je asimetrični kriptosustav koji su osmislili 1996. g. J. Hoffstein, J. Piper i J. H. Silverman. NTRU je vjerojatnosni kriptosustav koji radi s prstenom polinoma:

(7)

Temelji se na SVP-u te je zbog toga jedan od najboljih kandidata za korištenje u vrijeme kvantnih računala.

Parametri NTRU kriptosustava

Parametri koji određuju NTRU kriptosustav su:

N - duljina polinoma; polinomi u R su stupnja manjeg od N; prost broj
q - veliki modul; koeficijenti polinoma se reduciraju modulo q; cijeli broj
p - mali modul; cijeli broj ili polinom
D_F - prostor polinoma privatnog ključa
D_G - prostor polinoma javnog ključa
D_R - prostor maskirajućeg polinoma
D_M - prostor polinoma čistog teksta

Za navedene parametre mora vrijediti:

Parametri (N, p, q) su javno poznati,
Parametri p i q moraju biti relativno prosti,
Parametar N mora biti prost broj

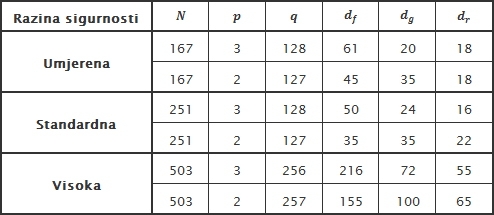
Prostori polinoma D_F , D_G , D_R i D_M definirani su vrijednostima d_F , d_G , d_R i d_M respektivno i sastoje se od polinoma čiji su koeficijenti iz skupa {-1,0,1} ili {0,1} ovisno o tome radi li se o ternarnim ili binarnim polinomima. U tablici 1 detaljnije su definirani pojedini prostori polinoma.

Tablica 1. Definiranje prostora polinoma

NTRU parametri preporučeni u [23] prikazani su u tablici 2.

Tablica 2. Preporučeni NTRU parametri

Generiranje ključeva

Generiranje ključeva počinje odabirom polinoma f iz D_F i polinoma g iz D_G . Zatim se računa inverz polinoma f modulo p i q:

(8)

Ako za odabrani f ne postoje inverzi, odabire se novi f dok se ne nađe onaj za kojeg postoje traženi inverzi. Javni ključ je polinom h:

(9)

Privatni ključ je par polinoma (f, f_p ).

Postupak kriptiranja

Kriptiranje se izvodi tako da se čisti tekst prebaci u polinomni oblik m iz skupa D_M , odnosno s koeficijentima reduciranima modulo p. Nakon toga se slučajnim odabirom generira polinom r iz D_Rte se uz pomoć javnog ključa računa kriptirana poruka e:

(10)

Postupak dekriptiranja

Dekriptiranje počinje upotrebom polinoma f:

(11)

Prilikom redukcije modulo q, koeficijenti se reduciraju na interval [-q/2, q/2], a ne na interval [0, q-1]. Nakon ovog koraka računa se redukcija polinoma modulo p i izvorna poruka:

(12)

(13)

Matematička pozadina

U prvom koraku postupka dekriptiranja zapravo se radi sljedeće:

Budući da su koeficijenti polinoma r, g, f i m mali, onda su i koeficijenti produkata r*g i f*m također mali, barem u odnosu na vrijednost q. Iz toga slijedi, ako su parametri dobro odabrani, da koeficijenti polinoma pr*g+f*m već leže unutar intervala [-q/2, q/2], pa redukcija modulo q nema nikakvog utjecaja. Nadalje, kada se radi redukcija polinoma a modulo p zapravo se radi redukcija polinoma pr*g+f*m modulo p, što daje b=f*m(mod p). U zadnjem koraku dekriptiranja upotrebljava se polinom f_p i računa se c=b*f_p(mod p)=m*f*f_p(mod p)=m(mod p).

Pogrešno dekriptiranje

U slučajevima kada koeficijenti polinoma pr*g+f*m uistinu jesu unutar intervala [-q/2, q/2], dekriptiranje će biti uspješno. Onda kada to nije slučaj, rezultat dekriptiranja biti će pogrešan. Pogrešno dekriptiranje je najveća mana NTRU kriptosustava i do pojave NAEP-a (Ntru Asymmetric Encryption Padding) pogrešno dekriptiranje se upotrebljavalo za napad [25] na privatni ključ.

Neka je max(a)=max_i(a_i), min(a)=min_i(a_i) i neka je širina polinoma jednaka width(a)=max(a)-min(a).

Dekriptiranje će biti pogrešno ako se dogodi:

Gap failure - ako je width(pr*g+f*m) >= q
Wrap failure - ako je width(pr*g+f*m)<q, ali je polinom reduciran u krivi interval

Wrap failure se izbjegava centriranjem polinoma, no još uvijek ne postoje metode za izbjegavanje gap failura. Vjerojatnost pogrešnog dekriptiranja (gap failura) jednaka je:

(14)

Centriranje polinoma izvodi se tako da se koeficijenti polinoma reduciraju na interval [A, A+q-1], gdje se vrijednost A računa na temelju relacije [23]:

(15)