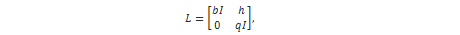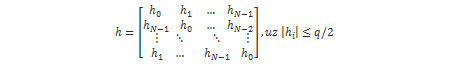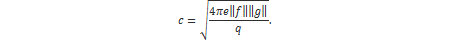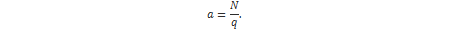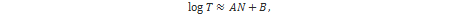Sigurnost NTRU kriptosustava
NTRU rešetka
Konvolucijska modularna rešetka je rešetka generirana retcima 2Nx2N matrice oblika:
(16)
gdje je I NxN jedinična matrica, q veliki modul, b konstanta balansa i h NxN matrica oblika:
(17)
Cikličko svojstvo konvolucijske modularne rešetke L označava da za svaki vektor rešetke v vrijedi, ako se koeficijenti vektora v ciklički pomaknu, dobiveni vektor v' je također sadržan u rešetki L.
Ako rešetka iz relacije (16) sadrži vektor oblika [f,g]=[f0 , f1 ,..., fN-1 , g0 , g1 ,..., gN-1] tada je rešetka iz (16) NTRU rešetka, oznake LNTRU .
Napad rešetkom
U praksi se pokazalo da su konstante koje najbolje pokazuju ovisnost duljine rješavanja CVP problema o dimenziji rešetke sljedeće:
(18)
(19)
U relaciji (18), ||x|| predstavlja 2-normu vektora x.
U praksi se pokazalo da održavanje konstante a i istovremeno povećanje konstante c drastično povećava vrijeme potrebno za redukciju rešetke. Isto tako pokazalo se da održavanje konstante c i povećanje konstante a neznatno smanjuje vrijeme potrebno za redukciju rešetke. [27]
Rješavanjem CVP-a konvolucijske modularne rešetke formirane od koeficijenata h(X)/p (mod q) dobiva se vektor v=[bv1,v2]=[bf(X),g(X)]. Pri tome je h(X) javni ključ, p mali modul i q veliki modul (sve javno poznate vrijednosti). Vrijednosti koje se traže su konstanta balansa, b i privatni ključ, f(X).
Heurističko vrijeme rješavanja
Neka je L modularna rešetka dimenzije n=2N, modula q i neka je (L,v) balansirani CVP rešetke L. Prosječno vrijeme T potrebno za rješavanje (L,v) je eksponencijalno u dimenziji s konstantama ovisnima o vrijednostima c i a opisanima ranije:
(20)
Uoči da log(T) zapravo predstavlja bitovnu razinu sigurnosti (engl. bit security).
U tablici 3 prikazani su eksperimentalni rezultati iz [27] za sigurnost NTRU-a s obzirom na napade rešetkama
Napad čovjek u sredini
Napad čovjek u sredini (engl. Meet In The Middle attack – MITM) kao i u drugim kriptosustavima, smanjuje prostor pretraživanja s drugim korijenom.
Ideja MITM napada [28] je naći polinom f u obliku f=f1+f2 , tako da polinom f1 ima prvih N/2 koeficijenata jednakih korespodentnim koeficijentima u polinomu f, a polinom f2 ima zadnjih N/2 koeficijenata jednakih korespodentnim koeficijentima u polinomu f. Oba polinoma f1 i f2 imaju df/2 jedinica. Iako f ne mora imati df/2 koeficijenata jednakih 1 na prvoj polovici polinoma, poznato je da je dovoljna jedna rotacija da se postigne takav raspored koeficijenata.
Upotrebljavajući relaciju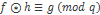 
dobiva se:
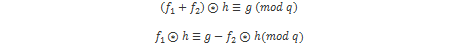(21)
Budući da polinom g ima koeficijente iz {0,1} ili {-1,0,1}, koeficijenti polinoma f1 * h i -f2 * h mogu se samo razlikovati za 0, 1 ili 2. S time u vidu napadač traži par (f1,f2) takav da isti koeficijenti imaju približno istu vrijednost. Detalji o ovom napadu mogu se vidjeti u pdf verziji rada.
Hibridni napad
Hibridni napad [29][30] je kombinacija napada rešetkom i napada čovjek u sredini. Hibridni napad je najefikasniji do danas poznat napad na NTRU kriptosustav, a detalji o njemu mogu se pogledati u pdf verziji rada.
 |
 |
 |