4. Prijava korisnika u Windows okruženju
U različitim se inačicama Windows operacijskog sustava sam izgled forme za prijavu korisnika mijenjao, ali je ideja uvijek ostala ista. Korisnik unosi korisničko ime i lozinku u formu, lozinka se kriptira algoritmom za izračunavanje sažetka poruke (eng. hash algorithm), te se dobiveni sažetak (eng. hash) uspoređuje s onim u bazi operacijskog sustava. Algoritam za izračunavanje sažetka jest matematička funkcija kojom se iz lozinke jednostavno dobiva njezin sažetak, ali je vrlo teško i vremenski zahtjevno (kod kvalitetnih algoritama, praktički nemoguće) iz sažetka dobiti originalnu vrijednost. Ako sažetak dobiven iz unesene lozinke odgovara sažetku u bazi uz uneseno korisničko ime, autentifikacija je uspjela, te je završen proces prijave. Teoretski postoji beskonačno mnogo lozinki koje daju isti sažetak, te nije potrebno unijeti ispravnu lozinku, nego samo lozinku koja daje isti sažetak. U praksi postoji konačno mnogo takvih lozinki zbog ograničenja duljine lozinke i mogućih znakova.
Ako lozinka ne odgovara, korisnik može pokušati ponovo. Nakon petog neuspjelog pokušaja, između svakog se pokušaja uvodi 30 sekundi pauze da bi se spriječilo ili barem usporilo pogađanje lozinke, bilo ručno ili automatski pomoću programa. Moguće je ograničiti broj pokušaja, vrijeme nakon kojeg se ponovno dozvoljava prijava i još nekoliko detalja. Detaljnije u poglavlju 6.
Daljnji tekst se bavi pretežno Windowsima do, uključivo, Windowsa XP. Vista je promijenila neke stvari, ali su neki kritični propusti ostali. Budući da su Windowsi XP najzastupljeniji u vrijeme pisanja seminara, nije veliki nedostatak što se Vista ne obrađuje u posebnoj cjelini.
4.1 Upravljanje sigurnošću korisničkih računa
Secutiry Account Manager (u daljnjem tekstu SAM) je baza podataka spremljena u Windows registryu na lokaciji "c:\windows\system32\config\sam" (umjesto windows, ovisno o verziji Windowsa te postavkama prilikom instalacije, može biti win, winnt ili nešto slično, u daljnjem će se tekstu umjesto različitih varijanti Windows direktorija koristiti oznaka %windir%). SAM sadrži podatke o korisnicima računala, sažetke lozinki, ovlasti, te još neke podatke koji trenutno nisu bitni. Sami sažeci lozinki su dobiveni korištenjem LM i NTLM algoritama, ali o njima više u poglavljima 4.1.1 i 4.1.2.
SAM je binarna datoteka čija struktura nikad nije javno objavljena, ali je svejedno otkrivena [2].
Primjer [3]:
000001f0: 6400 6f00 6d00 6100 6900 6e00 0102 0000 d.o.m.a.i.n.....
00000200: 0700 0000 0002 0000 0700 0000 ce28 297d .............()}
00000210: ede4 0fab 3a0f 6436 aff3 881f 0edb a361 ....:.d6.......a
00000220: 4fb6 c22a e367 e3ea bad8 807c 0edb a361 O..*.g.....|...a
Slika 4.1 – Dio SAM datoteke
Ovo je dio
SAM datoteke za administratorski račun. Lozinke počinju na adresi
0x20c. Prvih 16 okteta je
LM sažetak, a sljedećih 16 je
NTLM.
LM sažetak:
ce28297dede40fab3a0f6436aff3881f
NTLM sažetak:
0edba3614fb6c22ae367e3eabad8807c
Da bi se zaštitilo od ručnog uređivanja SAM-a, dakle dodavanja korisnika, mijenjanja lozinki, od Windowsa NT 4.0 SP2 uvedena su dva mehanizma zaštite. Jedna je nemogućnost kopiranja i otvaranja SAM-a dok Windowsi rade, osim programima pokrenutih sa administratorskim privilegijama, a drugi je kriptiranje samih podataka u SAM-u pomoću programa SYSKEY. Izgled datoteke je prilično sličan, samo se u njemu nalaze sažeci sažetaka lozinki, te su još dodatno razmaknuti graničnikom 0100 0000.
1999. godine Bindviewov [3] sigurnosni tim je razotkrio slabosti u načinu kriptiranja SAM-a. Kao rezultat toga uvedene su promjene u mehanizmu SYSKEY-a, te kao rezultat više nisu mogući (točnije, više nisu jednostavni) napadi grubom silom (eng. brute force) na SAM.
Za kriptiranje lozinke u SAM-u koriste se dva algoritma. Stariji LM (Lan Manager) koristio se u ranijim verzijama Windowsa. Kasnije je uveden novi, snažniji te fleksibilniji algoritam NTLM, ali je LM zadržan radi unazadne kompatibilnosti kod korištenja poslužitelja za pohranu podataka o korisničkim računima (eng. domain controllera), kako bi se mogla koristiti i računala s starijim verzijama Windowsa koje ne podržavaju NTLM. Moguće je u registryu isključiti pohranu lozinki u obliku LM sažetka, što bitno doprinosi sigurnosti. Više o postupku u poglavlju 6.
U slučaju LM-a, maksimalna duljina lozinke je 14 znakova (može biti i više, ali će se koristiti samo prvih 14), te može uključivati samo standardne alfanumeričke znakove engleskog jezika. U slučaju NTLM-a se mogu koristiti lozinke do 127 znakova te mogu sadržavati znakove drugih jezika te različite specijalne znakove. Sve zajedno u LM lozinkama može se koristiti približno 69 različitih znakova, dok je kod NTLM-a taj broj veći od 630 znakova.
NTLMv1 i NTLMv2 su nazivi za protokol autentifikacije korisnika kod korištenja domain controllera prilikom korištenja NTLM algoritma. Oba su protokola tipa izazov-odgovor, dok se za protokol kod korištenja LM sažetka koristi naziv LANMAN. Ali ovo je dio koji spada u područje mrežne sigurnosti.
4.1.1 LM algoritam i slabosti
Kriptiranje lozinke pomoću LM-a može se prikazati u 6 koraka [4]:
- Sva mala slova u lozinci se pretvaraju u velika.
- Ako je lozinka kraća od 14 znakova popunjava se sa NULL znakom (ACSII 0) do duljine od 14 znakova, a ako je duža od 14, reže se na 14 znakova.
- Lozinka se dijeli u dva dijela po 7 znakova.
- Te vrijednosti čine dva ključa u DES algoritmu.
- Oba ključa se koriste da bi se DES-om kriptirao ASCII niz "KGS!@#$%", te tako dobijemo dvije vrijednosti od po 8 okteta.
- Te se dvije vrijednosti spajaju da dobijemo 16 oktetni sažetak.
Primjer: za primjer ćemo iskoristiti lozinku koja zadovoljava većinu standarda za sigurne lozinke "Fer123reF". Lozinka sadrži mala, velika slova te brojke.
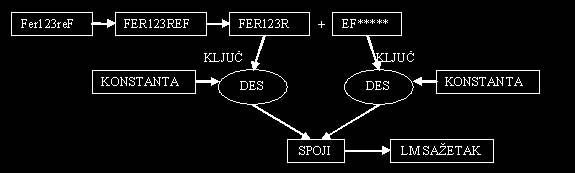
Slika 4.2 – Primjer rada LM algoritma
Iako je DES algoritam prilično siguran, LM sažetak može biti jednostavno provaljen zbog loše implementacije. Prvo, mijenjanje malih u velika slova umanjuje broj mogućih znakova, te zatim dijeljenje u dva dijela po 7 znakova omogućava da se svaki dio zasebno pokuša provaliti što znatno smanjuje mogući broj kombinacija. Ako pak lozinka ima sedam ili manje znakova, drugi dio sažetka je uvijek isti te ga se uopće ne treba probijati, jer je poznat sažetak. Više o samoj metodici provale u poglavlju 4.3.
4.1.2 NTLM algoritam
NTLM algoritam za izračunavanje sažetka je puno jednostavniji od LM-a. Uzme se lozinka te se kriptira MD4 algoritmom. Rezultat je 16 oktetni NTLM sažetak. MD4 algoritam je prilično siguran, te je implementacija korektno izvedena pa nema trivijalnih slabosti kao u LM algoritmu.
4.2 Manipulacije SAM-om
Manipulacije SAM-om možemo podijeliti u tri kategorije. Prva je zamjena SAM-a, koja uključuje zamjenu postojećeg SAM-a novim. Druga je modifikacije SAM-a, to jest umetanje novih korisnika ili mijenjanje lozinki. Treća je krađa SAM datoteke kako bi se mogla dekriptirati na nekom drugom računalu.
Problem sa zamjenom i modifikacijom SAM-a je da su promjene lako uočljive i jednokratne. Dakle, nakon što zamijenimo ili modificiramo SAM, uzmemo podatke koje smo htjeli, moramo vratiti stari SAM, osim ako nam nije bitno hoće li nas otkriti, te svaki put kad želimo ponovo pristupiti tom računalu moramo ponovo ponoviti cijelu proceduru. Puno je jednostavnije uzeti neki live operacijski sustav, pokrenuti ga, te pomoću njega pokupiti podatke koje želimo ili ukrasti SAM te ga negdje drugdje dekiptirati. Time se dobiva stalan pristup (ili, barem dok se ne promijene lozinke) tom računalu. Prve dvije tehnike su korisne ako ne možemo dekriptirati SAM, jer je LM isključen, a lozinke korisnika prekompleksne da bi se mogle probiti u nekom razumnom vremenu.
4.2.1 Zamjena SAM-a
Kako bi se mijenjao SAM potrebno je pokrenuti računalo bez pokretanja Windows operacijskog sustava. Ako je datotečni sustav Windows particije FAT, može se koristiti bilo koji live operacijski sustav ili instalacijski CD Windowsa. Ako je datotečni sustav NTFS mora se koristiti instalacijski CD Windowsa. Razlika je u tome što je NTFS zatvorena Microsoftova norma pa drugi operacijski sustavi ne mogu pristupiti tom datotečnom podsustavu, iako postoje projekti i aplikacije koje to omogućavaju, ali su još uvijek u stadiju testiranja i nisu pouzdani.
Ako želimo sustav podići s prijenosnog medija, potrebno je u BIOS-u promijeniti stavku Boot order (neke verzije BIOS-a dozvoljavaju da se prilikom podizanja računala pritisne neka tipka, nakon čega se ponudi izbornik s uređajima od kojih odaberemo onaj s kojeg želimo dići operativni sustav, na primjer na novijim računalima marke Dell to je F12). Lokacija stavke varira u različitim verzijama BIOS-a. Ako je BIOS zaštićen lozinkom potrebno je prvo nju zaobići, koristeći neku od ranije navedenih metoda u poglavlju 6. Potrebno je postaviti Boot order stavku na tip medija s kojeg planiramo dići operativni sustav (npr. CD-ROM za live CD). Jednako tako za pokretanje s Windows instalacijskog CD-a potrebno je postaviti boot order na CD-ROM te zatim ući u recovery konzolu.
Sljedeće dvije mogućnosti se mogu koristiti svejedno o operacijskom sustavu koji se koristi.
Potrebno se pozicionirati u direktorij u kojem se nalazi SAM te obrišemo datoteke "SAM" i "sam.log". Prilikom ponovnog pokretanja računala, Windowsi neće naći SAM te će automatski napraviti osnovnu SAM datoteku koji sadrži samo administratorski i gost račun. Gost račun je onemogućen, ali administratorski radi, te nema lozinke.
U direktorij gdje se nalazi SAM prekopiramo unaprijed pripremljene SAM config i SAM repair datoteke [5] na mjesto originalnih ("$windir$\system32\config" te "$windir$\repair", respektivno). Ako se kasnije potrebno vratiti na staro potrebno je pospremiti originalne datoteke u neki drugi direktorij te ih kasnije vratiti istim postupkom koji smo i sad koristili. Nakon ponovnog pokretanja računala moguće se prijaviti podacima iz novog SAM-a.
4.2.2 Modifikacija SAM-a
Ova tehnika uključuje promjenu lozinke nekog već postojećeg korisnika ili dodavanje posve novog. Ako nije uključen SYSKEY, što je vrlo malo vjerojatno, ovo je trivijalan zadatak. Ako je uključen, moguće je i onda, zbog slabosti algoritma koji se koristi za kriptiranje, ali se ove dvije tehnike danas uopće ne primjenjuju niti razvijaju, te su ovdje navedene čisto kao mogućnost.
4.2.3 Krađa SAM-a iz Windowsa
Za ovu se tehniku koristi alat pod imenom pwdump [6] trenutno u verziji 6. Pwdump uzima SAM, dekodira ga, te ga takvog sprema u svojem formatu. Pwdumpov format zapisa SAM-a se smatra de facto standardom, te svi programi koji se koriste za dekriptiranje SAM-a podržavaju ovaj oblik ulaza.
Administrator:500:NO PASSWORD*********************:NO PASSWORD*********************:::
Korisnik:1003:A9CA01E1A5D7D0F75C9C24C12E2C20AB:EC9193DE81246BCD685B47C9D995FC44:::
Guest:501:NO PASSWORD*********************:NO PASSWORD*********************:::
Slika 4.3 – Dio izlaza iz pwdumpa
Format izlaza je u obliku
<korisničko ime>:<identifikacijski broj>:<LM sažetak>:<NTLM sažetak>:<komentar>:<korisnički direktorij>
Kako bi pwdump radio, potrebno ga je pokrenuti s administratorskim privilegijama, što znači da treba biti pokrenut na računalu na kojem je trenutno aktivan administratorski račun.
Način rada pwdumpa je prilično kompliciran ali se može ukratko opisati. Pwdump se pokreće kao servis, te koristi tehniku injekcije DLL-a da stekne debug privilegije, te zatim pomoću ugrađene i nedokumentirane interne Windows funkcije prikupi podatke o svim korisnicima. Iako su mu podaci poslani kriptirani, prilikom pokretanja servisa, Windowsi mu predaju ključ potreban za dekriptiranje.
4.2.4 Krađa SAM-a pomoću live CD-a
Kod ove tehnike prvo treba pribaviti ključ korišten kod SYSKEY enkripcije. Taj problem uspješno rješava program po imenu bkhive [7] koji koristi slabosti kod implementacije algoritma. Naime ključ korišten kod enkripcije je permutacija ključeva koji su slobodno dostupni u registryu.
Nakon što smo pomoću bkhivea pribavili ključ, pomoću programa samdump, kojem kao ulazi argument predamo ključ, dobijemo dekriptirani SAM u pwdump formatu koji možemo pospremiti na neki prijenosni medij [8].
Postoji alat, orphcrack [9], koji implementira oba gore navedena alata. Dostupan je kao alat koji se pokreće na Windowsima, Linuxu ili Mac OS-u, te kao live CD. On automatski pribavlja SYSKEY, SAM, te automatski počinje dekriptiranje SAM-a pomoću rainbow tablica, koje su obrađene u poglavlju 4.3.2.
4.3 Dekriptiranje SAM-a
Dobivanje lozinki iz sažetaka koji se nalaze u SAM-u nazivat ćemo dekriptiranjem SAM-a. Postoji tri osnovne tehnike. Gruba sila, napad rječnikom te rainbow tablice. Prve dvije ćemo samo površno spomenuti, te ćemo se detaljnije pozabaviti trećom.
4.3.1 Gruba sila i napad rječnikom
Napad grubom silom sastoji se od generiranja svih mogućih kombinacija mogućih lozinki, ili nekog podskupa, na primjer sve lozinke duže od šest znakova, kriptiranja istih te usporedbe odgovaraju li sažetku lozinke dobivene iz SAM-a. Problem ove tehnike je vrijeme. Napad može trajati od dugo za LM sažetak, pa do praktički beskonačno za NTLM sažetak.
Napad rječnikom je metoda u kojoj se koristi lista najčešće upotrebljavanih riječi (ili svih riječi nekog jezika) koje se zatim kriptiraju te se uspoređuju s sažetkom lozinke. Postoji i modifikacija rječničkog napada u kojoj se na kraj riječi stavljaju brojevi ili specijalni znakovi.
Uspješnost rječničke metode proizlazi iz neupućenosti samih korisnika. Korisnici će za lozinku najvjerojatnije odabrati neku riječ, radije nego nasumičan niz slova i brojka. Ako se nakon nekog vremena promijeni sigurnosna politika tvrtke pa se poveća minimalna duljina lozinke, te se odredi da lozinka mora sadržavati broj ili specijalni znak, korisnici će najvjerojatnije na kraj postojeće lozinke dodati neki znak.
Neki od poznatijih alata za ove dvije metode napada su Cain and Abel [10]. Cain and Abel je alat koji podržava različite metode provala, nekoliko desetaka različitih sažetaka koje probija te je cjeloviti alat za testiranje sigurnosti Windows operacijskih sustava. Tu je još i John the Ripper [11], koji je open source projekt dostupan u različitim varijantama i za različite platforme te L0phtcrack [12] koji je alat razvijan pod kapom Symanteca ali je 2006. godine prekinut rad na njemu.
4.3.2 Rainbow tablice
Rainbow tablice koriste se kako bi se iz zadanog sažetka dobila početna vrijednost. Prvi put su predstavljene u radu "Making a Faster Cryptanalytic Time-Memory Trade-Off" Philippea Oechslina [13]. Postoje dvije krajnosti u probijanju sažetaka. Prva je da svaki put kad želimo probiti takvu vrijednost generiramo sve mogućnosti. Druga je da samo jednom generiramo sve mogućnosti te ih spremimo, pa kasnije samo pretražujemo po njima. Problem je prve tehnike vremenska složenost, a druge prostorna. Rainbow tablice uzimaju najbolje iz oba pristupa.
Za razumijevanje rainbow tablice bitna su dva pojma. Prvi je funkcija za izračunavanje sažetka poruke, već gore objašnjena, ali ovdje na uz mali dodatak. Funkcija sažetka je funkcija koja iz nekog niz znakova (eng. plaintext) dobiva niz binarnih vrijednosti (eng. hash). Označit čemo ju s S(x). Druga funkcija je funkcija redukcije, koja iz binarne vrijednosti dobiva niz znakova. Označavat ćemo ju s R(x).
Funkcija redukcije nije, niti ne može biti inverz funkcije sažetka, zbog svojstva funkcije sažetka da ne postoji inverz. Također funkcije redukcije nisu jedinstvene.
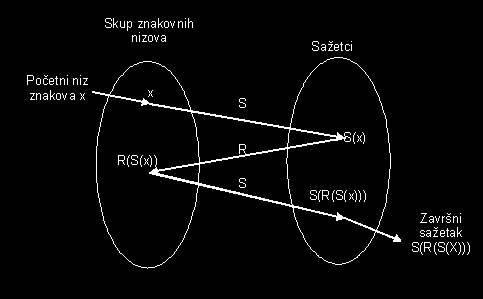
Slika 4.4 – Princip rada rainbow tablica
Pojednostavljeni algoritam stvaranja rainbow tablica:
- U tablicu dodati početni niz znakova.
- Primijeniti nad nizom znakova funkciju sažetka.
- Ako je izvršen maksimalan broj iteracija, u tablicu pokraj početnog niza znakova zapisati zadnji dobiveni sažetak, te završiti. Inače, produžiti na korak 4.
- Primijeniti funkciju redukcije na sažetak, te produžiti na korak 2.
Lista koja se sastoji od početnog niza te svih sažetaka dobivenih u procesu naziva se lanac.
Pojednostavljenje gornjeg algoritma je u tome da rainbow tablice koriste više stupaca, dakle više funkcija redukcije, te se gornji algoritam sukladno tome proširuje. U svakom se stupcu nalazi završni sažetak dobiven različitom funkcijom redukcije. Ovaj pristup rješava problem izražen kod prijašnjih postupaka sa sličnom idejom. Postoji mogućnost da funkcija redukcije kreira neku vrijednost koja se već nalazi u tom lancu pa dolazimo do petlje te nećemo pokriti sve sažetke. Druga stvar koju ovaj pristup postiže je da iz jednog početnog niza razriješimo više sažetaka.
Iz samog načina stvaranja rainbow tablice vidi se da nisu nužno pokriveni svi mogući sažetci. Zato se uz rainbow tablice redovito navodi postotak uspješnosti razrješavanja zadanog sažetka. Postotak uspješnosti ponajviše ovisi o kvaliteti algoritama redukcije.
Pojednostavljeni algoritam pretraživanja >rainbow tablice:
- Provjeriti da li se zadani sažetak nalazi u tablici. Ako da, produžiti na korak 4 pamteći početnu vrijednost lanca za koji je pronađen sažetak, inače produžiti na korak 2.
- Ako je izvršen maksimalan broj iteracija, javiti da traženi sažetak nije pronađen.
- Primijeniti nad sažetkom funkciju redukcije i funkciju sažetka te produžiti na korak 1.
- Primijeniti funkciju sažetka nad ulaznim nizom. Ako dobiveni sažetak odgovara traženom, vratiti kao rezultat ulazni niz. Inače produžiti na korak 5.
- Primijeniti nad ulaznim nizom funkciju redukcije te produžiti na korak 4.
Pojednostavljenje ovog algoritma je isto kao i u algoritmu stvaranja, dakle u tome da se pretpostavlja samo jedna funkcija redukcije, ali se iz ovako pojednostavljenog algoritma dobro vidi princip pretraživanja rainbow tablice.
Primjer: Generirat ćemo jednostavnu rainbow tablicu sa dva lanca duljine 3. Funkcija sažetka i funkcija redukcije nisu bitne. Duljina sažetka neka je 2 okteta, a niza 5 znakova. S označava primjenu funkcije sažetka, a R funkcije redukcije nad nizom u prvom susjednom polju na lijevo. Koristiti će se samo jedna funkciju redukcije.
Tablica 4.1 – Proces generiranja rainbow tablice
| Početni niz |
S |
S |
S |
S |
S |
| df13x |
23A1 |
kyz22 |
110F |
nmqi |
FFE1 |
| cmw11 |
62F3 |
gkaj0 |
00D1 |
fja24 |
451B |
Nakon što je algoritamom završio, rainbow tablica ima sljedeći oblik:
Tablica 4.2 – Završni izgled rainbow tablice
| Početni niz |
Završni sažetak |
| df13x |
FFE1 |
| cmw11 |
451B |
Pretpostavimo da se traži niz kojemu odgovara sažetak 00D1.
00D1 se ne nalazi u tablici. Nad njim se primjeni funkcija redukcije i dobiva se vrijednost fja24 te se zatim primjenom funkcije sažetaka dobiva 451B, koji se nalazi u tablici.
Uzima se početni niz kojemu odgovara završni sažetak 451B, u ovom slučaju cmw11, te se nad njime primijeni funkcija sažetka. Dobiva se 62F3 koji ne odgovara ulaznom sažetku.
Primjenom funkcije redukcije nad 62F3, dobiva se gkaj0, te se zapamti taj niz. Primjenom funkcije sažetka na njime, dobiva se 00D1, što je traženi sažetak. Niz od kojeg je dobiven traženi sažetak, gkaj0, je dakle rješenje.
Postoji mnogo besplatnih rainbow tablica za LM algoritam dok se kvalitetne NTLM pretežno prodaju. Neke od boljih rainbow tablica za LM algoritam su dostupne na sljedeće dvije Internet stranice:
Prva garantira probijanje svih LM sažetaka, te je velika 120gb. Na drugoj je stranici dostupno više verzija sortiranih po dužini, te znakovima koje podržavaju.
Spomenimo dodatno jedan od popularnijih alata za generiranje rainbow tablica pod imenom Winrtgen [14]. U trenutnoj verziji, 2.3, podržava generiranje rainbow tablica za devetnaest različitih funkcija za izračunavanje sažetka, među kojima su i nama interesantni LM i NTLM.

